
分析 如图所示,当四边形PMQN为正方形且MN⊥OP时,|MN|取得最小值或最大值,求出M的坐标即可得出结论.
解答 解:如图所示, 当四边形PMQN为正方形且MN⊥OP时,|MN|取得最小值或最大值.
当四边形PMQN为正方形且MN⊥OP时,|MN|取得最小值或最大值.
设kPM=k,∵∠QPM=45°,∴$\frac{2-k}{1+2k}$=1,解得k=$\frac{1}{3}$.
∴直线PM的方程为:y-2=$\frac{1}{3}$(x-1),化为x-3y+5=0,
代入圆 的方程,化为10y2-30y+9=0,
解得y=$\frac{15+3\sqrt{15}}{10}$或y=$\frac{15-3\sqrt{15}}{10}$.
∴x=3y-5=$\frac{9\sqrt{15}-5}{10}$或$\frac{-9\sqrt{15}-5}{10}$.
∵MN=$\sqrt{2}$PM
∴MNmin=3$\sqrt{3}$-$\sqrt{5}$,MNmax=3$\sqrt{3}$+$\sqrt{5}$.
故答案为:[3$\sqrt{3}$-$\sqrt{5}$,3$\sqrt{3}$+$\sqrt{5}$].
点评 本题考查了向量的平行四边形法则和矩形的定义、满足一定条件取得最小值的转化问题,考查了计算能力,属于难题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-3,-1] | C. | (-1,1] | D. | [-3,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 135° | C. | 45°或135° | D. | 45° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{2}{5}$ | C. | -2 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
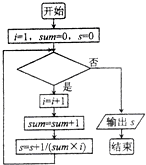
| A. | i≤5? | B. | i≤4? | C. | i≥4? | D. | i≥5? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com