
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
, ![]() 为椭圆
为椭圆![]() 的右顶点,
的右顶点, ![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的上、下顶点.线段
的上、下顶点.线段![]() 的延长线与线段
的延长线与线段![]() 交于点
交于点![]() ,与椭圆
,与椭圆![]() 交于点
交于点![]() .(1)若椭圆的离心率为
.(1)若椭圆的离心率为![]() ,
, ![]() 的面积为12,求椭圆
的面积为12,求椭圆![]() 的方程;(2)设
的方程;(2)设![]() ,求实数
,求实数![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1CAC1
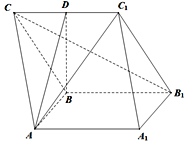
(Ⅰ)求证:平面AA1B1B面BB1C1C;
(Ⅱ)若D是CC1中点,ADB是二面角A-CC1-B的平面角,求直线AC1与平面ABC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 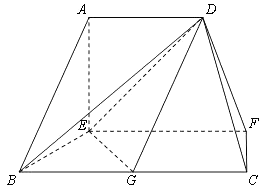
(1)求证:AB∥平面DEG;
(2)求证:BD⊥EG;
(3)求二面角C﹣DF﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意实数x,y满足f(x)+f(y)=f(x+y)+3,f(3)=6,当x>0 时,f(x)>3,那么,当f(2a+1)<5时,实数a的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+c的图像如图,直线y=0在原点处与函数图像相切,且此切线与函数图像所围成的区域(阴影)面积为 ![]() .
. 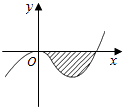
(1)求f(x)的解析式
(2)若常数m>0,求函数f(x)在区间[﹣m,m]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知f(x)=x2﹣2x+2,在[ ![]() ,m2﹣m+2]上任取三个数a,b,c,均存在以 f(a),f(b),f(c)为三边的三角形,则m的取值范围为( )
,m2﹣m+2]上任取三个数a,b,c,均存在以 f(a),f(b),f(c)为三边的三角形,则m的取值范围为( )
A.(0,1)
B.[0, ![]() )
)
C.(0, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名同学在5次英语口语测试中的成绩统计如图的茎叶图所示.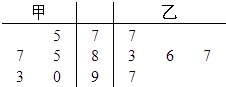
(注:样本数据x1 , x2 , …,xn的方差s2= ![]() [
[ ![]() +
+ ![]() +…+
+…+ ![]() ],其中
],其中 ![]() 表示样本均值)
表示样本均值)
(1)现要从中选派一人参加英语口语竞赛,从两同学的平均成绩和方差分析,派谁参加更合适;
(2)若将频率视为概率,对学生甲在今后的三次英语口语竞赛成绩进行预测,记这三次成绩中高于80分的次数为ξ,求ξ的分布列及数学期望Eξ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com