
����Ŀ���ס�������ͬѧ��5��Ӣ���������еijɼ�ͳ����ͼ�ľ�Ҷͼ��ʾ��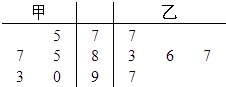
��ע����������x1 �� x2 �� ����xn�ķ���s2= ![]() [
[ ![]() +
+ ![]() +��+
+��+ ![]() ]������
]������ ![]() ��ʾ������ֵ��
��ʾ������ֵ��
��1����Ҫ����ѡ��һ�˲μ�Ӣ����ᄎ��������ͬѧ��ƽ���ɼ��ͷ����������˭�μӸ����ʣ�
��2������Ƶ����Ϊ���ʣ���ѧ�����ڽ�������Ӣ����ᄎ���ɼ�����Ԥ�⣬�������γɼ��и���80�ֵĴ���Ϊ�Σ���εķֲ��м���ѧ����E�Σ�
���𰸡�
��1��
�⣺ ![]() =
= ![]() =86����1�֣���
=86����1�֣��� ![]() =
= ![]() =86��
=86��
![]() =
= ![]() =37.6
=37.6
![]() =
= ![]() =42.4
=42.4
��Ϊ ![]() ��
�� ![]() ��
�� ![]() �������ɼ�ȥ������
�������ɼ�ȥ������
��2��
�⣺����80�ֵ�Ƶ��Ϊ ![]() ���Ӷ�ÿ�γɼ�����80�ֵĸ���P=
���Ӷ�ÿ�γɼ�����80�ֵĸ���P= ![]()
��ȡֵΪ0��1��2��3���Ρ���3�� ![]() ��
��
ֱ�Ӽ����P����=0��= ![]() =
= ![]() ��P����=1��=
��P����=1��= ![]() =
= ![]() ��
��
P����=2��= ![]() =
= ![]() ��P����=3��=
��P����=3��= ![]() =
= ![]() ��
��
�εķֲ���Ϊ
�� | 0 | 1 | 2 | 3 |
P |
|
|
|
|
���ԣ�E��=0�� ![]() +1��
+1�� ![]() +2��
+2�� ![]() +3��
+3�� ![]() =
= ![]()
����������1�����ݾ�Ҷͼ�����ݣ�����ƽ���������ʽ��������ý��ۣ���2����æ�ȡֵ���Ρ���3�� ![]() ���������Ӧ���ʣ��ɵæεķֲ��У��Ӷ�������ѧ����E�Σ�
���������Ӧ���ʣ��ɵæεķֲ��У��Ӷ�������ѧ����E�Σ�
�����㾫�����������⣬������Ҫ�˽⾥Ҷͼ(��Ҷͼ�ֳơ�֦Ҷͼ��������˼·�ǽ������е�����λ�����бȽϣ������Ĵ�С���������仯�����λ��Ϊһ�����ɣ����������仯���λ������Ϊ��֦��Ҷ�����������ɵĺ��棬�����Ϳ�������ؿ���ÿ�����ɺ���ļ�������ÿ���������Ƕ���)����Ҫ����ƽ��������λ��������(��ƽ��������������λ����������һ�����ݼ������Ƶ�������ƽ��������������λ�����е�λ����ƽ������ӳһ�����ݵ�ƽ��ˮƽ�������������е�ÿ�������й�ϵ��������Ϊ��Ҫ��Ӧ����㣻����λ�����ܸ���ƫ���ƫС���ݵ�Ӱ�죻��������������ݳ��ֵ�Ƶ���йأ����ܸ������ݵ�Ӱ�죬��ʱ��������Ϊ���ĵ�����)�����֪ʶ���Ǵ���Ĺؼ���


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д� ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]()
![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() ��
�� ![]() Ϊ��Բ
Ϊ��Բ![]() ���Ҷ��㣬
���Ҷ��㣬 ![]() ��
�� ![]() �ֱ�Ϊ��Բ
�ֱ�Ϊ��Բ![]() ���ϡ��¶���.�߶�
���ϡ��¶���.�߶�![]() ���ӳ������߶�
���ӳ������߶�![]() ���ڵ�
���ڵ�![]() ������Բ
������Բ![]() ���ڵ�
���ڵ�![]() .��1������Բ��������Ϊ
.��1������Բ��������Ϊ![]() ��
�� ![]() �����Ϊ12������Բ
�����Ϊ12������Բ![]() �ķ��̣���2����
�ķ��̣���2����![]() ����ʵ��
����ʵ��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ ��
��![]() Ϊ���������ڼ�����ϵ����ƽ��ֱ������ϵ
Ϊ���������ڼ�����ϵ����ƽ��ֱ������ϵ![]() ȡ��ͬ�ij��ȵ�λ������ԭ��
ȡ��ͬ�ij��ȵ�λ������ԭ��![]() Ϊ���㣬��
Ϊ���㣬��![]() ��Ǹ�����Ϊ���ᣩ�У�ֱ��
��Ǹ�����Ϊ���ᣩ�У�ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��
��1��������![]() ����ͨ���̼�ֱ��
����ͨ���̼�ֱ��![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2����![]() ������
������![]() �ϵ�����һ�㣬���
�ϵ�����һ�㣬���![]() ��ֱ��
��ֱ��![]() �ľ�������ֵ��
�ľ�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]()
��1������ ![]() �Ķ�����
�Ķ�����
��2��������a��R�������� ![]() ���ܴ���Ψһx0��[��1��2]��ʹ��f��x1��=g��x0����������ʵ��a��ȡֵ��Χ��
���ܴ���Ψһx0��[��1��2]��ʹ��f��x1��=g��x0����������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={x|��2��x��5}��B={x|m��4��x��3m+3}��
��1����AB����ʵ��m��ȡֵ��Χ��
��2����A��B=B����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ķ���
�ڵ�ʽcos2x=2cos2x��1��x��R�����������ã���cos2x����=��2cos2x��1���䣬�����ã���sin2x��2=4cosx����sinx��������õ�ʽ��sin2x=2cosxsinx��
��1������������뷨������������������ϵ�ʽ��1+x��n=Cn0+Cn1x+Cn2x2+��+Cnnxn��x��R��������n��2����֤���� ![]() ��
��
��2������������n��3����֤��
��i�� ![]() ��
��
��ii�� ![]() ��
��
��iii�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵ��溯��f��x��= 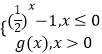 ����f��1��=������ʽf��f��x������7�Ľ⼯Ϊ ��
����f��1��=������ʽf��f��x������7�Ľ⼯Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��0��a��1������f��x��=loga��x+1���� ![]() ����F��x��=2f��x��+g��x��
����F��x��=2f��x��+g��x��
��1������F��x���Ķ�����D������㣻
��2�������ۺ���F��x���ڶ�����D�ϵĵ����ԣ�
��3��������x�ķ���F��x����2m2+3m+5=0������[0��1���ڽ���һ�⣬��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����min{a��b��c}��ʾa��b��c�������е���Сֵ����f��x��=min{2x �� x+2��10��x}��x��0������f��x�������ֵΪ�� ��
A.7
B.6
C.5
D.4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com