
分析 利用导数的概念变形得出$\underset{lim}{x→a}$$\frac{af(x)-af(a)+af(a)-xf(a)}{x-a}$=$\underset{lim}{x→a}$[a$\frac{f(x)-f(a)}{x-a}$-f(a)],根据极限式子可判断为af′(a)-f(a).
解答 解:∵$\underset{lim}{x→a}$$\frac{af(x)-xf(a)}{x-a}$=$\underset{lim}{x→a}$$\frac{af(x)-af(a)+af(a)-xf(a)}{x-a}$=$\underset{lim}{x→a}$[a$\frac{f(x)-f(a)}{x-a}$-f(a)]=a$\underset{lim}{x→a}$$\frac{f(x)-f(a)}{x-a}$-f(a)=af′(a)-f(a).
∴$\underset{lim}{x→a}$$\frac{af(x)-xf(a)}{x-a}$=af′(a)-f(a).
点评 本题考查了导数的概念,性质,运用,关键是恒等变形得出需要的式子,可判断出答案.


科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{8}$ | B. | -$\frac{\sqrt{15}}{8}$ | C. | 1 | D. | $\frac{\sqrt{15}}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
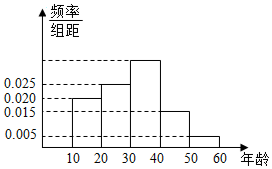 随机抽取100名年龄在[10,20),[20,30)…,[50,60)年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于30岁的人中按年龄段分层抽样的方法随机抽取22人,则在[50,60)年龄段抽取的人数为2.
随机抽取100名年龄在[10,20),[20,30)…,[50,60)年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于30岁的人中按年龄段分层抽样的方法随机抽取22人,则在[50,60)年龄段抽取的人数为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{{\sqrt{5}}}{3}]$ | B. | $[\frac{{\sqrt{5}}}{3},1)$ | C. | $(0,\frac{{\sqrt{3}}}{2}]$ | D. | $[\frac{{\sqrt{3}}}{2},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $-\frac{3}{2}$ | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com