分析:(1)取CD的中点K,连结MK,NK,由线面平行的判定结合中位线定理,证出MK∥面ADD
1A
1,NK∥面ADD
1A
1,利用面面平行判定定理得到面MNK∥面ADD
1A
1,结合MN?面MNK,证出MN∥面ADD
1A
1;
(2)取A
1D
1的中点F,连结AF、EF,可得平行四边形CEFD
1中EF∥CD
1,得∠AEF(或其补角)为异面直线AE和CD
1所成的角.△AEF中算出AE、AF、EF的长,利用余弦定理算出
cos∠AEF=,即得异面直线AE和CD
1所成角的余弦值.
解答:解:

(Ⅰ)取CD的中点K,连结MK,NK
∵长方体ABCD-A
1B
1C
1D
1中,M、N、K分别为AK、CD
1、CD的中点
∴MK∥AD,NK∥DD
1 ∵MK、NK?面ADD
1A
1,AD?面ADD
1A
1,DD
1?面ADD
1A
1,
∴MK∥面ADD
1A
1,NK∥面ADD
1A
1∵MK、NK是平面MNK内的相交直线
∴面MNK∥面ADD
1A
1 又∵MN?面MNK,∴MN∥面ADD
1A
1;
(Ⅱ)取A
1D
1的中点F,连结AF、EF,
则
D1FCE,从而四边形CEFD
1为平行四边形,
∴EF∥CD
1,可得∠AEF(或其补角)为异面直线AE和CD
1所成的角
在△AEF中,可得
AF=,
AE=,
EF=CD1=a 由余弦定理,得
cos∠AEF== ∴异面直线AE和CD
1所成角的余弦值为
.
点评:本题给出长方体中,求证线面平行并求异面直线所成的角.着重考查了线面平行、面面平行的判定与性质,考查了异面直线所成角的定义和余弦定理等知识,属于中档题.

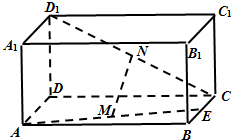 如图,长方体ABCD-A1B1C1D1中,E是BC的中点,M,N分别是AE,CD1的中点,AD=AA1=a,AB=2a,
如图,长方体ABCD-A1B1C1D1中,E是BC的中点,M,N分别是AE,CD1的中点,AD=AA1=a,AB=2a, (Ⅰ)取CD的中点K,连结MK,NK
(Ⅰ)取CD的中点K,连结MK,NK 

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 15、如图,长方体ABCD-A1B1C1D1中被截去一部分,
15、如图,长方体ABCD-A1B1C1D1中被截去一部分, 如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中
如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中 如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.
如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点. 已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )
已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )