
分析 (1)求出f′(x)=lnx-2ax+1,由此利用导数的几何意义能出过点(1,f(1))的切线方程.
(2)令g(x)=f′(x)=lnx-2ax+1,则${g}^{'}(x)=\frac{1-2ax}{x}$,由此利用导数性质及分类讨论思想能求出a的取值范围.
(3)0<a<$\frac{1}{2}$时,f(x)有两个极值点x1,x2,f(x)在(0,x1)上递减,在(x1,x2)上递增,在(x2,+∞)上递减,令h(x)=lnx+1-2x2,(0<x<1),${h}^{'}(x)=\frac{1-4{x}^{2}}{x}$,由此利用导数性质能求出f(x)的最小值.
解答 解:(1)∵函数f(x)=x(lnx-ax),
∴f′(x)=lnx-2ax+1,…(1分)
当a=$\frac{1}{2}$ 时,f′(1)=0,且f(1)=-$\frac{1}{2}$,
∴过点(1,f(1))的切线方程为y=-$\frac{1}{2}$.…4 分
(2)令g(x)=f′(x)=lnx-2ax+1,则${g}^{'}(x)=\frac{1-2ax}{x}$,
当a≤0时,g′(x)>0,g(x)在(0,+∞)上单调递增,
g(x)与X轴只有一个交点即f(x)只有一个极值点,不合题意.…(5分)
当a>0时,x∈(0,$\frac{1}{2a}$)时,g′(x)>0,g(x)在(0,$\frac{1}{2a}$)上递增,
x∈($\frac{1}{2a},+∞$)时,g′(x)<0,g(x)在($\frac{1}{2a},+∞$)上递减,
只需g($\frac{1}{2a}$)=ln$\frac{1}{2a}$>0,即0<a<$\frac{1}{2}$时,f(x)有两个极值点
故0<a<$\frac{1}{2}$.…(8分)
(3)由(2)知 0<a<$\frac{1}{2}$时,f(x)有两个极值点x1,x2,
f(x)在(0,x1)上递减,在(x1,x2)上递增,在(x2,+∞)上递减,
又f′(1)=1-2a>0,则0<x1<1,且lnx1-2ax1+1=0,
解得a=$\frac{ln{x}_{1}+1}{2{x}_{1}}$,此时a-x1=$\frac{ln{x}_{1}+1-2{{x}_{1}}^{2}}{2{x}_{1}}$,…(10分)
令h(x)=lnx+1-2x2,(0<x<1),${h}^{'}(x)=\frac{1-4{x}^{2}}{x}$,
从而h(x)在(0,$\frac{1}{2}$)上递增,($\frac{1}{2}$,1)上递减,
故h(x)≤h($\frac{1}{2}$)=ln$\frac{1}{2}+\frac{1}{2}<0$,
所以a<x1,又f(x)在(0,x1)上递减,
从而f(x)的最小值为f(a)=a(lna-a2).…(12分)
点评 本题考查切线方程的求法,考查实数的取值范围的求法,考查函数的最小值的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:选择题
| A. | 左平移$\frac{π}{12}$ | B. | 左平移$\frac{π}{6}$ | C. | 右平移$\frac{π}{12}$ | D. | 右平移$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为${a_{ij}}(i≥j,i,j∈{N^*})$,则a63=( )
如图给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为${a_{ij}}(i≥j,i,j∈{N^*})$,则a63=( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=1,点M是SD的重点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=1,点M是SD的重点,AN⊥SC,且交SC于点N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4p2 | B. | -3p2 | C. | -2p2 | D. | -p2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-6,-2] | B. | $[-6,-\frac{9}{8}]$ | C. | [-5,-3] | D. | [-4,-3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
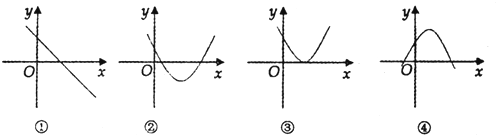
| A. | ①③ | B. | ②③ | C. | ①②④ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com