
 如图给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为${a_{ij}}(i≥j,i,j∈{N^*})$,则a63=( )
如图给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为${a_{ij}}(i≥j,i,j∈{N^*})$,则a63=( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 先确定ai1,再求出aij=$\frac{i}{3}$×($\frac{1}{2}$)j-1,即可得到结论.
解答 解:由题意,每一列的数成等差数列,首项$\frac{1}{3}$,公差为$\frac{1}{3}$
∴ai1=$\frac{1}{3}$+(i-1)•$\frac{1}{3}$=$\frac{i}{3}$,
每一行的数成等比数列,公比为$\frac{1}{2}$,
∴aij=ai1×($\frac{1}{2}$)j-1=$\frac{i}{3}$×($\frac{1}{2}$)j-1.
∴a63=2×($\frac{1}{2}$)2=$\frac{1}{2}$.
故选C.
点评 本题考查等差数列和等比数列的性质,考查了考生分析问题和解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
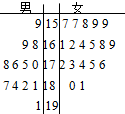 第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行,为工作需要,组委会拟定组建一个“五人接待小组”,先在各中学进行海选,招募了12名男生和18名女生志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:cm).若身高
第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行,为工作需要,组委会拟定组建一个“五人接待小组”,先在各中学进行海选,招募了12名男生和18名女生志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:cm).若身高查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<0,f(b)<0 | B. | f(a)>0,f(b)>0 | C. | f(a)<0,f(b)>0 | D. | f(a)>0,f(b)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第一行 | 1 | 3 | 5 | 7 | |
| 第二行 | 15 | 13 | 11 | 9 | |
| 第三行 | 17 | 19 | 21 | 23 | |
| … | … | 27 | 25 |
| A. | 第253行第1列 | B. | 第253行第2列 | C. | 第252行第3列 | D. | 第254行第2列 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com