
分析 (1)求出a=1时f(x)的导数,可得切线的斜率和切点,运用点斜式方程,即可得到所求切线方程;
(2)假设存在实数a,使得f(x)=ax-lnx,x∈(0,e]的最小值为3,对a讨论:当a≤0时,当$0<\frac{1}{a}<e$,即$a>\frac{1}{e}$时,当$\frac{1}{a}≥e$,即$0<a≤\frac{1}{e}$时,求出单调区间,可得最小值,解方程即可得到所求a的值.
解答 解:(1)当a=1时,函数f(x)=x-lnx的导数为$f'(x)=1-\frac{1}{x}$,
所以切线斜率$k=f'(e)=\frac{e-1}{e},f(e)=e-1$,
所以切线方程为$y-(e-1)=\frac{e-1}{e}(x-e)$,
即$y=\frac{e-1}{e}x$.
(2)假设存在实数a,使得f(x)=ax-lnx,x∈(0,e]的最小值为3,
$f'(x)=a-\frac{1}{x}=\frac{ax-1}{x}$,0<x≤e,
①当a≤0时,因为x∈(0,e],所以f'(x)<0,
所以f(x)在(0,e]上单调递减,f(x)min=f(e)=ae-1=3得$a=\frac{4}{e}$(舍去);
②当$0<\frac{1}{a}<e$,即$a>\frac{1}{e}$时,f(x)在$(0,\frac{1}{a})$上单调递减,在$({\frac{1}{a},e}]$上单调递增,$f{(x)_{min}}=f(\frac{1}{a})=1+lna=3$得a=e2满足.
③当$\frac{1}{a}≥e$,即$0<a≤\frac{1}{e}$时,因为x∈(0,e],所以f'(x)≤0,
所以f(x)在(0,e]上单调递减,f(x)min=f(e)=ae-1=3,得$a=\frac{4}{e}$(舍去).
综上,存在实数a=e2满足题意.
点评 本题考查导数的运用:求切线方程和单调区间、极值和最值,考查存在性问题的解法,同时考查分类讨论思想方法,化简整理运算能力,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{2x}{x}$与y=2 | B. | y=$\sqrt{{x}^{2}}$与y=($\sqrt{x}$)2 | C. | y=lgx2与y=2lgx | D. | y=$\frac{{x}^{2}}{x}$与y=x(x≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
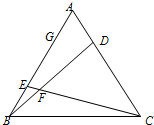 如图,正△ABC中,点D在边AC上,E,G在边AB上,且AB=3AG=6,AD=λAC,AE=(1-λ)AB,(0<λ<1),BD,CE相交于点F
如图,正△ABC中,点D在边AC上,E,G在边AB上,且AB=3AG=6,AD=λAC,AE=(1-λ)AB,(0<λ<1),BD,CE相交于点F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
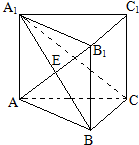 已知ABC-A1B1C1为直三棱柱,AB⊥BC,AA1=AB=BC,连接AB1交A1B于点E,
已知ABC-A1B1C1为直三棱柱,AB⊥BC,AA1=AB=BC,连接AB1交A1B于点E,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1<-2 | B. | x2>0 | C. | x3<1 | D. | x3>2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com