
| A. | y=$\frac{2x}{x}$与y=2 | B. | y=$\sqrt{{x}^{2}}$与y=($\sqrt{x}$)2 | C. | y=lgx2与y=2lgx | D. | y=$\frac{{x}^{2}}{x}$与y=x(x≠0) |
分析 由定义域相同,对应关系相同,是同一函数,依次判断可知A,B,C均不是,D为同一函数.
解答 解:对于A,y=$\frac{2x}{x}$=2(x≠0)与y=2,定义域不同,不是同一函数;
对于B,y=$\sqrt{{x}^{2}}$=|x|,与y=($\sqrt{x}$)2=x,(x≥0)定义域不同,对应关系不同,不是同一函数;
对于C,y=lgx2与y=2lgx,前者定义域为{x|x≠0},后者定义域为{x|x>0},不是同一函数;
对于D,y=$\frac{{x}^{2}}{x}$=x(x≠0)与y=x(x≠0),定义域相同,对应关系相同,是同一函数.
故选:D.
点评 本题考查同一函数的判断,只要定义域相同,对应关系相同,就是同一函数,属于基础题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:填空题
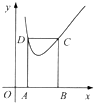 如图,矩形ABCD的边AB在x轴上,顶点C,D在函数y=x+$\frac{1}{x}({x>0})$的图象上.记AB=m,BC=n,则$\frac{m}{n^2}$的最大值为$\frac{1}{4}$.
如图,矩形ABCD的边AB在x轴上,顶点C,D在函数y=x+$\frac{1}{x}({x>0})$的图象上.记AB=m,BC=n,则$\frac{m}{n^2}$的最大值为$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 1或-2 | D. | 1或-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-∞,-1)∪(0,1) | D. | (-1,0)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 左平移$\frac{π}{12}$ | B. | 左平移$\frac{π}{6}$ | C. | 右平移$\frac{π}{12}$ | D. | 右平移$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com