
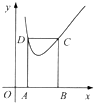
 如图,矩形ABCD的边AB在x轴上,顶点C,D在函数y=x+$\frac{1}{x}({x>0})$的图象上.记AB=m,BC=n,则$\frac{m}{n^2}$的最大值为$\frac{1}{4}$.
如图,矩形ABCD的边AB在x轴上,顶点C,D在函数y=x+$\frac{1}{x}({x>0})$的图象上.记AB=m,BC=n,则$\frac{m}{n^2}$的最大值为$\frac{1}{4}$. 分析 设C(x1,y1),D(x2,y2),把C,D的坐标代入函数解析式,得到x1x2=1,再代入$\frac{m}{n^2}$,利用换元法结合二次函数求最值.
解答 解:设C(x1,y1),D(x2,y2),
∵y1=y2,${x}_{1}+\frac{1}{{x}_{1}}={x}_{2}+\frac{1}{{x}_{2}}$,x1≠x2,
∴x1x2=1.
∴$\frac{m}{n^2}$=$\frac{{x}_{2}-{x}_{1}}{({x}_{2}+\frac{1}{{x}_{2}})^{2}}=\frac{{x}_{2}-\frac{1}{{x}_{2}}}{({x}_{2}+\frac{1}{{x}_{2}})^{2}}=\frac{t}{{t}^{2}+4}$$≤\frac{1}{4}$,$t={x}_{2}-\frac{1}{{x}_{2}}>0$,
当且仅当t=2时成立.
故答案为:$\frac{1}{4}$.
点评 本题考查对勾函数,考查了函数值域的求法,考查数学转化思想方法,属中档题.


科目:高中数学 来源: 题型:解答题
 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1(-1,0),F2(1,0),上、下顶点分别为B1、B2,右准线l:x=4.
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1(-1,0),F2(1,0),上、下顶点分别为B1、B2,右准线l:x=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
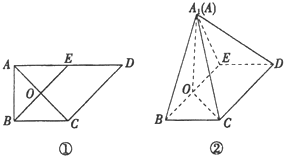 如图①,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=$\sqrt{2}$,AD=2$\sqrt{2}$,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图②.
如图①,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=$\sqrt{2}$,AD=2$\sqrt{2}$,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图②.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{17}}{2}$ | B. | $\frac{\sqrt{15}}{3}$ | C. | $\frac{\sqrt{57}}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | 4 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 1 | C. | 5$\sqrt{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<e≤$\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$≤e<1 | C. | $\frac{\sqrt{3}}{2}$<e<1 | D. | $\frac{\sqrt{3}}{2}$≤e<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{24}$ | D. | $\frac{1}{120}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{2x}{x}$与y=2 | B. | y=$\sqrt{{x}^{2}}$与y=($\sqrt{x}$)2 | C. | y=lgx2与y=2lgx | D. | y=$\frac{{x}^{2}}{x}$与y=x(x≠0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com