
 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1(-1,0),F2(1,0),上、下顶点分别为B1、B2,右准线l:x=4.
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1(-1,0),F2(1,0),上、下顶点分别为B1、B2,右准线l:x=4.分析 (1)由题意可知:椭圆的焦点在x轴上,c=1,准线方程x=$\frac{{a}^{2}}{c}$=4,即a=2,b2=a2-c2=3,即可求得椭圆的方程;
(2)直线B1M方程为:y=-$\sqrt{3}$x+$\sqrt{3}$,代入椭圆方程,求得点M($\frac{8}{5}$,$\frac{-3\sqrt{3}}{5}$),直线B2M方程为:y=$\frac{1}{4}$$\sqrt{3}$x-$\sqrt{3}$,当x=4,求得y=0,即可求得点N的坐标;
(3)A点的坐标为(-a,0),B点坐标为(0,b),a2+b2=μ2,$\frac{丨\overrightarrow{AQ}丨}{丨\overrightarrow{QB}丨}$=λ,设Q点坐标为(x,y),则-x=$\frac{丨\overrightarrow{QB}丨}{丨\overrightarrow{AB}丨}$•丨$\overrightarrow{AO}$丨=$\frac{1}{λ+1}$a,y=$\frac{丨\overrightarrow{AQ}丨}{丨\overrightarrow{AB}丨}$•b=$\frac{λ}{λ+1}$b,代入椭圆方程,整理可知:当4λ2-3=0时,即当λ=$\frac{\sqrt{3}}{2}$时,3μ2=12(λ+1)2,即可求得常数λ,μ的值.
解答 解:(1)由题意可知:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)椭圆的焦点在x轴上,
由c=1,准线方程x=$\frac{{a}^{2}}{c}$=4,即a=2,
由b2=a2-c2=3,
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)直线B1M方程为:y=-$\sqrt{3}$x+$\sqrt{3}$,
代入椭圆方程,求得点M($\frac{8}{5}$,$\frac{-3\sqrt{3}}{5}$),
直线B2M方程为:y=$\frac{1}{4}$$\sqrt{3}$x-$\sqrt{3}$,
代入椭圆方程,当x=4,求得y=0,
∴N(-4,0),
(3)如图可知:A点的坐标为(-a,0),B点坐标为(0,b),
由a2+b2=μ2,
由$\frac{丨\overrightarrow{AQ}丨}{丨\overrightarrow{QB}丨}$=λ,
设Q点坐标为(x,y),则-x=$\frac{丨\overrightarrow{QB}丨}{丨\overrightarrow{AB}丨}$•丨$\overrightarrow{AO}$丨=$\frac{1}{λ+1}$a,
y=$\frac{丨\overrightarrow{AQ}丨}{丨\overrightarrow{AB}丨}$•b=$\frac{λ}{λ+1}$b,
∵Q在椭圆上,则Q(x,y)满足椭圆方程,
$\frac{3{a}^{2}}{(λ+1)^{2}}$+$\frac{{λ}^{2}{b}^{2}}{(λ+1)^{2}}$=12,整理得:3a2+4λ2b2=12(λ+1)2,
由a2+b2=μ2,则a2=μ2-b2,
代入整理得:3(μ2-b2)+4λ2b2=12(λ+1)2,即3μ2+(4λ2-3)b2=12(λ+1)2,
∴当4λ2-3=0时,即当λ=$\frac{\sqrt{3}}{2}$时,
3μ2=12(λ+1)2,
则μ=4(λ+1)2,即μ=$\sqrt{3}$+2,
∴当λ=$\frac{\sqrt{3}}{2}$,总有$\overrightarrow{AQ}$=λ$\overrightarrow{QB}$且AB=μ=$\sqrt{3}$+2.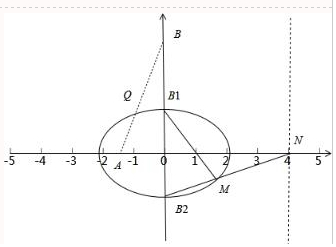
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆位置关系,考查抽象概括能力、推理论证能力、运算求解能力,考查数形结合思想与函数与方程思想的应用,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
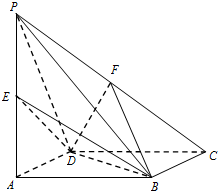 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[5-2\sqrt{2},5+2\sqrt{2}]$ | B. | $[\sqrt{5},\sqrt{29}]$ | C. | $[\sqrt{5},\sqrt{61}]$ | D. | $[\sqrt{29},\sqrt{61}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
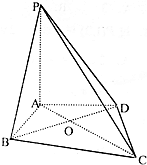 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BCD=60°,DC=BC=$\sqrt{3}$,AC和BD交于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BCD=60°,DC=BC=$\sqrt{3}$,AC和BD交于O点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别 是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别 是PC,PD,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,3] | B. | [-1,3] | C. | [1,+∞)∪(-∞,-3] | D. | [3,+∞)∪(-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
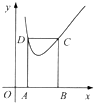 如图,矩形ABCD的边AB在x轴上,顶点C,D在函数y=x+$\frac{1}{x}({x>0})$的图象上.记AB=m,BC=n,则$\frac{m}{n^2}$的最大值为$\frac{1}{4}$.
如图,矩形ABCD的边AB在x轴上,顶点C,D在函数y=x+$\frac{1}{x}({x>0})$的图象上.记AB=m,BC=n,则$\frac{m}{n^2}$的最大值为$\frac{1}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com