
分析 (1)先确定函数的定义域然后求导数f′(x),令g(x)=2x2+2x+a,由题意知x1、x2是方程g(x)=0的两个均大于-1的不相等的实根,建立不等关系解之即可,在函数的定义域内解不等式f′(x)>0和f′(x)<0,求出单调区间;
(2)x2是方程g(x)=0的根,将a用x2表示,消去a得到关于x2的函数,研究函数的单调性求出函数的最大值,即可求f(x2)的取值范围.
解答 解:(1)求导函数可得f′(x)=$\frac{{x}^{2}+x+a}{x+1}$(x>-1)
令g(x)=x2+x+a,其对称轴为x=-$\frac{1}{2}$,
由题意知x1、x2是方程g(x)=0的两个均大于-1的不相等的实根,
其充要条件为△=4-4a>0且g(-1)=a>0,得0<a<$\frac{1}{4}$…(2分)
①当x∈(-1,x1)时,f'(x)>0,∴f(x)在(-1,x1)内为增函数;
②当x∈(x1,x2)时,f'(x)<0,∴f(x)在(x1,x2)内为减函数;
③当x∈(x2,+∞)时,f'(x)>0,∴f(x)在(x2,+∞)内为增函数;
(2)由(1)g(0)=a>0,∴-$\frac{1}{2}$<x2<0,a=-(x22+x2)
∴f(x2)=$\frac{1}{2}$x22+aln(1+x2)=$\frac{1}{2}$x22-(x22+x2)ln(1+x2)
设h(x)=x2-(2x2+2x)ln(1+x)(x>-$\frac{1}{2}$),…(8分)
则h'(x)=2x-2(2x+1)ln(1+x)-2x=-2(2x+1)ln(1+x)…(10分)
①当x∈(-$\frac{1}{2}$,0)时,h'(x)>0,∴h(x)在(-$\frac{1}{2}$,0)单调递增;
②当x∈(0,+∞)时,h'(x)<0,h(x)在(0,+∞)单调递减 …(12分)
∴当x∈(-$\frac{1}{2}$,0)时,h(x)>h(-$\frac{1}{2}$)=$\frac{1-2ln2}{4}$,
故f(x2)=$\frac{1}{2}$h(x2)>$\frac{1-2ln2}{8}$. …(14分)
点评 本题主要考查了利用导数研究函数的单调性,以及利用导数研究函数的极值等有关知识,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
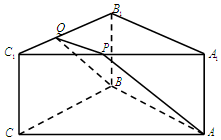 如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).
如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
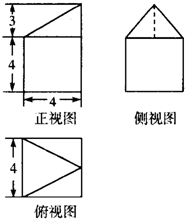
| A. | 98+6$\sqrt{5}$ | B. | 106+6$\sqrt{5}$ | C. | 114+6$\sqrt{5}$ | D. | 106+12$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com