
分析 ①根据平面向量的数量积公式和模长公式,得出$\overrightarrow{a}$、$\overrightarrow{b}$共线,即$\overrightarrow{b}$=t$\overrightarrow{a}$;
②数列{an}是等差数列时,由am+an=as+at不能得出m+n=s+t;
③举例说明等比数列an=(-1)n时,S6,S12-S6,S18-S12不是等比数列;
④由$\frac{1}{tanA}$,$\frac{1}{tanB}$,$\frac{1}{tanC}$依次成等差数列,得出a2,b2,c2也成等差数列.
解答 解:对于①,非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,
∴${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=${|\overrightarrow{a}|}^{2}$+2|$\overrightarrow{a}$|×|$\overrightarrow{b}$|+${|\overrightarrow{b}|}^{2}$,
∴-2|$\overrightarrow{a}$|×|$\overrightarrow{b}$|cosθ=2|$\overrightarrow{a}$|×|$\overrightarrow{b}$|,
∴cosθ=-1,∴$\overrightarrow{a}$、$\overrightarrow{b}$共线,
即存在实数t,使得$\overrightarrow{b}$=t$\overrightarrow{a}$成立,①正确;
对于②,数列{an}是等差数列,且am+an=as+at(m、n、s、t∈N*),
∴a1+(m-1)d+a1+(n-1)d=a1+(s-1d)+a1+(n-1)d,
∴(m+n)d=(s+t)d;
当d≠0时,m+n=s+t,
当d=0时,m+n=s+t不成立,∴②错误;
对于③,设an=(-1)n,
则S6=0,S12-S6=0,S18-S12=0,
∴此数列不是等比数列,③错误;
对于④,△ABC中,$\frac{1}{tanA}$,$\frac{1}{tanB}$,$\frac{1}{tanC}$依次成等差数列,
∴$\frac{2}{tanB}$=$\frac{1}{tanA}$+$\frac{1}{tanC}$,
∴2cosBsinAsinC=cosAsinBsinC+cosCsinAsinB,
由正弦定理,得
2accosB=bccosA+abcosC=b(ccosA+acosC),
由余弦定理,得a2+c2-b2=$\frac{1}{2}$(b2+c2-a2)+$\frac{1}{2}$(a2+b2-c2)
∴a2+c2=2b2,a2,b2,c2成等差数列,④正确.
综上,正确的命题序号是①④.
故答案为:①④.
点评 本题考查了命题真假的判断问题,也考查了平面向量以及等差、等比数列的应用问题,是综合题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,5+2$\sqrt{2}$] | B. | (-∞,8] | C. | [$\frac{26}{3}$,+∞) | D. | (-∞,5+2$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -sin(lnx) | B. | $\frac{sin(lnx)}{x}$ | C. | -$\frac{sin(lnx)}{x}$ | D. | $\frac{cos(lnx)}{x}$ |
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(文)试卷(解析版) 题型:选择题
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
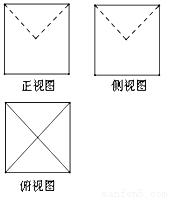
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com