
| A. | 3 | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
分析 由$\overrightarrow{a}⊥\overrightarrow{b}$便得到$\overrightarrow{a}•\overrightarrow{b}=0$,而再由$|\overrightarrow{a}|=1,|\overrightarrow{b}|=2$即可求出$(\overrightarrow{a}-\overrightarrow{b})^{2}$的值,进而便可得出$|\overrightarrow{a}-\overrightarrow{b}|$的值.
解答 解:∵$\overrightarrow{a}⊥\overrightarrow{b}$;
∴$\overrightarrow{a}•\overrightarrow{b}=0$;
∴$(\overrightarrow{a}-\overrightarrow{b})^{2}={\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=1-0+4=5;
∴$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{5}$.
故选C.
点评 考查向量垂直的充要条件,向量数量积的运算,以及要求$|\overrightarrow{a}-\overrightarrow{b}|$而求$(\overrightarrow{a}-\overrightarrow{b})^{2}$的方法.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 6 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
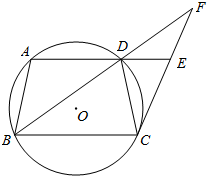 如图,梯形ABCD内接于圆O,AD∥BC,过点C作圆O的切线,交BD的延长线于点F,交AD的延长线于点E.
如图,梯形ABCD内接于圆O,AD∥BC,过点C作圆O的切线,交BD的延长线于点F,交AD的延长线于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com