Question

12．设x、y满足约束条件$\left\{\begin{array}{l}{|2x-y|≤2}\\{|2x+y|≤2}\end{array}\right.$，则z=2^x+y的最小值是$\frac{1}{4}$．

Answer 1

分析 由约束条件作出可行域，令t=x+y，化为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入求得t的最小值，则z=2^x+y的最小值可求．

解答 解：由约束条件$\left\{\begin{array}{l}{|2x-y|≤2}\\{|2x+y|≤2}\end{array}\right.$作出可行域如图，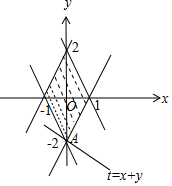

令t=x+y，化为y=-x+t，由图可知，当直线y=-x+t过A（0，-2）时，直线在y轴上的截距最小，t有最小值为-2．
∴z=2^x+y的最小值是${2}^{-2}=\frac{1}{4}$．
故答案为：$\frac{1}{4}$．

点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．