
���� ��1��������֪�������г����������Բ�ļ����������ɵõ������
��2�������MΪ��ԲC�ġ�2�ֵ㡰������S��AOB=2S��AOD����ֱ��l�ķ���Ϊx=my+x0��������Բ���̣�����Τ�ﶨ�������㼴�ɵõ�����Χ��
��� �⣺��1��������F1��F2�ֱ�Ϊ��ԲE��$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0�������ҽ��㣬
��DΪ��ԲE���㣬��|CD|=$\sqrt{5}$����Բ��������Ϊ$\frac{{\sqrt{3}}}{2}$��
�ɵã�${a^2}+{b^2}=5��\frac{{\sqrt{3}}}{2}=\sqrt{1-\frac{b^2}{a^2}}$��a2=4��b2=1��
��ԲE�ķ���Ϊ$\frac{x^2}{4}+{y^2}=1$��
��2������M����ԲE�ġ�2�ֵ㡱��
����ڹ���M��ֱ��l����ԲE����A��B���㣬ʹ��S��AOB=2S��AOD��
��Ȼֱ��l��y�ᴹֱ����l��x=my+1��A��x1��y1����B��x2��y2����
��$\left\{\begin{array}{l}\frac{x^2}{4}+{y^2}=1\\ x=my+1\end{array}\right.$���ã�m2+4��y2+2my-3=0������${y_1}+{y_2}=\frac{-2m}{{{m^2}+4}}$����${y_1}{y_2}=\frac{-3}{{{m^2}+4}}$����
��ΪS��AOB=2S��AOD����$\frac{1}{2}��{|{y_1}|+|{y_2}|}��=2��\frac{1}{2}��2|{y_1}|����|{y_2}|=3|{y_1}|$��
�ɢ�֪y1y2��0����y2=-3y1���۽��۴���ٵ�${y_1}=\frac{m}{{{m^2}+4}}$����
���۴���ڵ�$y_1^2=\frac{1}{{{m^2}+4}}$���ݽ��ܴ���ݵ�$\frac{m^2}{{{m^2}+4}}=1$���⣮
���Ե�M��1��0��������ԲE�ġ�2�ֵ㡱��
���� ������Ҫ�����¶������������ã�������Բ�ķ��̺����ʣ�ͬʱ��������ֱ�߷��̺���Բ���̣�����Τ�ﶨ�����������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
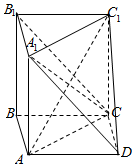 ��ͼ��ʾ�ļ������У�������ABC-A1B1C1Ϊֱ��������ABCDΪƽ���ı��Σ�AD=2CD����ADC=60�㣮
��ͼ��ʾ�ļ������У�������ABC-A1B1C1Ϊֱ��������ABCDΪƽ���ı��Σ�AD=2CD����ADC=60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2}$ | B�� | $\frac{1}{2}$ | C�� | -$\frac{\sqrt{3}}{2}$ | D�� | $\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{2}}{2}$ | B�� | $\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | $\frac{\sqrt{6}}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
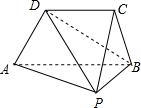 ��ͼ������P-ABCD��DC��AB��PB��AB��ƽ��PAB��ƽ��ABCD��AD=DC=CB=1��AB=BP=2
��ͼ������P-ABCD��DC��AB��PB��AB��ƽ��PAB��ƽ��ABCD��AD=DC=CB=1��AB=BP=2�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢ڢ� | B�� | �٢ۢ� | C�� | �ڢۢ� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com