
分析 根据所给不等式,即可类比得出结论.
解答 解:根据①sinx1=sinx1
②sinx1+sinx2≤2sin$\frac{{{x_1}+{x_2}}}{2}$
③sinx1+sinx2+sinx3≤3sin$\frac{{{x_1}+{x_2}+{x_3}}}{3}$
④sinx1+sinx2+sinx3+sinx4≤4sin$\frac{{{x_1}+{x_2}+{x_3}+{x_4}}}{4}$
猜想得到一般的结论是$sin{x_1}+sin{x_2}+…+sin{x_n}≤nsin\frac{{{x_1}+{x_2}+…+{x_n}}}{n}$.
故答案为:$sin{x_1}+sin{x_2}+…+sin{x_n}≤nsin\frac{{{x_1}+{x_2}+…+{x_n}}}{n}$.
点评 合情推理中的类比推理是指依据两类数学对象的相似性,将已知的一类数学对象的性质类比迁移到另一类数学对象上去.其思维过程大致是:观察、比较 联想、类推 猜测新的结论.结论的正确与否,必须经过证明.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24种 | B. | 48种 | C. | 36种 | D. | 28种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
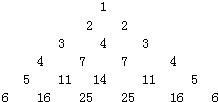 (两选一)
(两选一)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 5+4$\sqrt{3}$ | C. | 7 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $±\sqrt{2}$ | C. | $\root{4}{2}$ | D. | ±$\root{4}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com