
某音乐喷泉喷射的水珠呈抛物线形,它在每分钟内随时间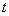 (秒)的变化规律大致可用
(秒)的变化规律大致可用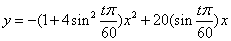 (
(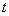 为时间参数,
为时间参数,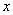 的单位:
的单位: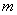 )来描述,其中地面可作为
)来描述,其中地面可作为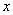 轴所在平面,泉眼为坐标原点,垂直于地面的直线为
轴所在平面,泉眼为坐标原点,垂直于地面的直线为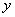 轴。
轴。
(Ⅰ)试求此喷泉喷射的圆形范围的半径最大值;
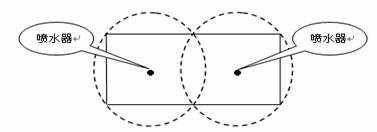
(Ⅱ)若在一建筑物前计划修建一个矩形花坛并在花坛内装置两个这样的喷泉,则如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?
 全能练考卷系列答案
全能练考卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com