
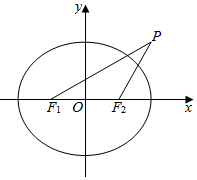
 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,焦距为2,设点P(a,b)满足△PF1F2是等腰三角形.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,焦距为2,设点P(a,b)满足△PF1F2是等腰三角形.分析 (Ⅰ)根据题意,有$\left\{{\begin{array}{l}{2c=2}\\{{{(a-1)}^2}+{b^2}=4}\end{array}}\right.$,由此能求出椭圆方程.
(Ⅱ)联立方程组$\left\{{\begin{array}{l}{y=k(x-m)}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$,得:(3+4k2)x2-8k2mx+4m2-12=0,由此利用根的判别式、韦达定理、弦长公式,结合已知条件推导出|MA|2+|MB|2=7与m无关符合题意.
解答 (本题15分)
解:(Ⅰ)∵椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,焦距为2,
设点P(a,b)满足△PF1F2是等腰三角形,
∴根据题意,有$\left\{{\begin{array}{l}{2c=2}\\{{{(a-1)}^2}+{b^2}=4}\end{array}}\right.$…(4分)
解得:$\left\{{\begin{array}{l}{a=2}\\{b=\sqrt{3}}\end{array}}\right.$,
故所求椭圆方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(6分)
(Ⅱ)联立方程:$\left\{{\begin{array}{l}{y=k(x-m)}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$,整理得:(3+4k2)x2-8k2mx+4m2-12=0
在△>0的情况下有:$\left\{{\begin{array}{l}{{x_1}+{x_2}=\frac{{8{k^2}m}}{{3+4{k^2}}}}\\{{x_1}{x_2}=\frac{{4{m^2}-12}}{{3+4{k^2}}}}\end{array}}\right.$…(9分)
$\begin{array}{l}|MA{|^2}+|MB{|^2}=(1+{k^2})[{({x_1}-m)^2}+{({x_2}-m)^2}]\\=(1+{k^2})[{({x_1}+{x_2})^2}-2{x_1}{x_2}-2m({x_1}+{x_2})+2{m^2}]\\=\frac{{(1+{k^2})}}{{{{(3+4{k^2})}^2}}}[(-24{k^2}+18){m^2}+96{k^2}+72]\end{array}$
令-24k2+18=0,得${k^2}=\frac{3}{4}$,即$k=±\frac{{\sqrt{3}}}{2}$…(13分)
此时|MA|2+|MB|2=7与m无关符合题意,…(15分)
点评 本题考查椭圆方程的求法,考查满足条件的实数是否存在的判断与证明,是中档题,解题时要认真审题,注意根的判别式、韦达定理、弦长公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | N⊆M | B. | M⊆N | C. | M∩N=∅ | D. | M∪N=R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{\sqrt{2}}{2}$,1) | D. | [$\frac{\sqrt{2}}{2}$,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com