
 ABC的边长为1,AE
ABC的边长为1,AE 平面ABC,CD∥AE,且CD=
平面ABC,CD∥AE,且CD=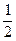 AE.
AE.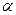 ,AE=
,AE=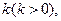 若
若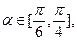 求
求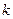 的取值范围;
的取值范围;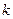 取得最大值时,求平面BDE与平面ABC所成角的大小.
取得最大值时,求平面BDE与平面ABC所成角的大小.

 方法一:
方法一: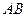 中点
中点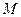 ,连结
,连结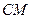 、
、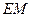 ,由
,由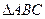 为正三角形,得
为正三角形,得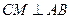 ,又
,又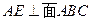 ,则
,则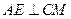 ,可知
,可知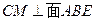 ,所以
,所以 为
为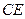 与平面
与平面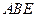 所成角.……………2分
所成角.……………2分 ,……………4分
,……………4分 ,得
,得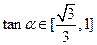 ,得
,得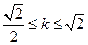 .……………6分
.……………6分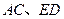 交于点S,连
交于点S,连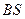 ,
,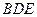
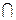 平面
平面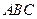 =
=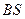 .………………………7分
.………………………7分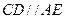 ,且
,且 ,又因为
,又因为 =1,从而
=1,从而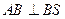 ,…………………8分
,…………………8分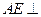 面
面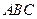 ,由三垂线定理可知
,由三垂线定理可知 ,即
,即 为平面
为平面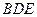 与平面
与平面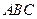 所成的角;……………………10分
所成的角;……………………10分 ,
,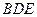 与面
与面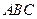 所成的角的大小为
所成的角的大小为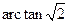 .………………12分
.………………12分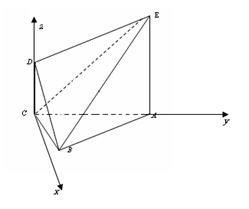 解:
解: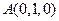 ,
,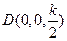 ,
,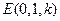 ,
,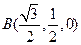 .……………2分
.……………2分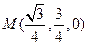 ,
,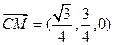 ,
,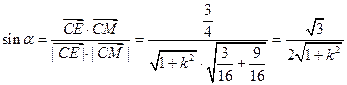 .………………4分
.………………4分 ,则
,则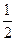
 ,
, 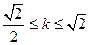 .…………………6分
.…………………6分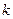 最大值为
最大值为 ,则当
,则当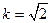 时,设平面BDE法向量为
时,设平面BDE法向量为 ,则
,则
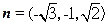 ,………………8分
,………………8分 ,……………………10分
,……………………10分 =
=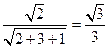 ,
,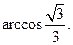 ……………………12分
……………………12分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
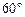 ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
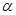 ,
,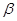 ,
,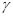 两两互相垂直,点
两两互相垂直,点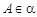 ,点
,点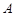 到
到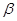 ,
,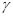 的距离都是
的距离都是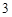 ,点
,点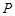 是
是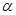 上的动点,满足
上的动点,满足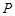 到
到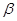 的距离是到
的距离是到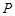 到点
到点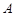 距离的
距离的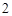 倍,则点
倍,则点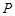 的轨迹上的点到
的轨迹上的点到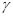 的距离的最小值为
的距离的最小值为A.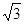 | B.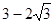 |
C.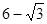 | D.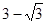 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.-a+ b+c b+c | B.a-b+c | C.a+b-c | D.a+b-c |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
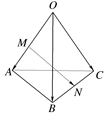
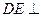 平面ABCD,
平面ABCD,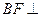 平面ABCD,且FB=2DE=2。
平面ABCD,且FB=2DE=2。
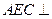 平面AFC。
平面AFC。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com