
(本小题14分)如图,在平面直角坐标系xoy中,设点F(0, p)(p>0), 直线l : y= -p, 点P在直线l上移动,R是线段PF与x轴的交点, 过R、P分别作直线 、
、 ,使
,使 ,
,
 .
.
(1) 求动点 的轨迹
的轨迹 的方程;
的方程;
(2)在直线 上任取一点
上任取一点 做曲线
做曲线 的两条切线,设切点为
的两条切线,设切点为 、
、 ,求证:直线
,求证:直线 恒过一定点.
恒过一定点.
解:(1) 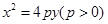 .(2)见解析.
.(2)见解析.
解析试题分析:(Ⅰ)先判断RQ是线段FP的垂直平分线,从而可得动点Q的轨迹C是以F为焦点,l为准线的抛物线;
(Ⅱ)设M(m,-p),两切点为A(x1,y1),B(x2,y2),求出切线方程,从而可得x1,x2为方程x2-2mx-4p2=0的两根,进一步可得直线AB的方程,即可得到直线恒过定点(0,p);
解:(1)依题意知,点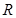 是线段
是线段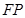 的中点,且
的中点,且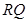 ⊥
⊥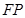 ,
,
∴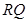 是线段
是线段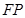 的垂直平分线. ∴
的垂直平分线. ∴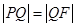 .
.
故动点 的轨迹
的轨迹 是以
是以 为焦点,
为焦点, 为准线的抛物线,
为准线的抛物线,
其方程为: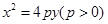 .
.
(2)设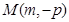 ,两切点为
,两切点为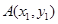 ,
,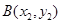
∴两条切线方程为x x=2p(y+y
x=2p(y+y ) ①
) ①
x x=2p(y+y
x=2p(y+y ) ②
) ②
对于方程①,代入点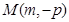 , 又
, 又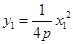 , 整理得:
, 整理得: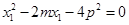 , 同理对方程②有
, 同理对方程②有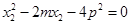 , 即
, 即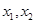 为方程
为方程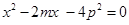 的两根.
的两根.
∴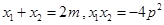 ③
③
设直线 的斜率为
的斜率为 ,
,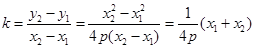
所以直线 的方程为
的方程为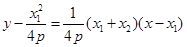 ,展开得:
,展开得: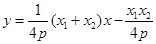 ,代入③得:
,代入③得: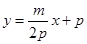 , ∴直线恒过定点
, ∴直线恒过定点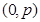 .
.
考点:本题主要考查了抛物线的定义,考查直线恒过定点,考查直线的向量,,属于中档题.
点评:解决该试题的关键是正确运用圆锥曲线的定义和韦达定理,来表示根与系数的关系的运用。


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
(本题满分16分)已知直线 :
:
(1)求证:不论实数 取何值,直线
取何值,直线 总经过一定点.
总经过一定点.
(2)为使直线不经过第二象限,求实数 的取值范围.
的取值范围.
(3)若直线 与两坐标轴的正半轴围成的三角形面积最小,求
与两坐标轴的正半轴围成的三角形面积最小,求 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
如图,已知三角形的顶点为A(2, 4),B(0,-2),C(-2,3),
求:
(Ⅰ)AB边上的中线CM所在直线的一般方程;
(Ⅱ)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)在 中,已知BC边上的高所在直线的方程为
中,已知BC边上的高所在直线的方程为 ,
, 平分线所在直线的方程为
平分线所在直线的方程为 ,若点B的坐标为(1,2),
,若点B的坐标为(1,2),
(Ⅰ)求直线BC的方程;
(Ⅱ)求点C的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知直线 的方程为
的方程为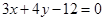 , 求直线
, 求直线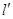 的方程, 使得:
的方程, 使得:
(1) 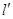 与
与 平行, 且过点(-1,3) ;
平行, 且过点(-1,3) ;
(2) 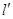 与
与 垂直, 且
垂直, 且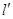 与两轴围成的三角形面积为4.
与两轴围成的三角形面积为4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com