Question

5．如图，在四边形ABCD中，∠BAD=90°，∠ADC=120°，AD=DC=2，AB=4，动点M在△BCD内（含边界）运动，设$\overrightarrow{AM}$=$λ\overrightarrow{AB}$+μ$\overrightarrow{AD}$，则λ+μ的取值范围是[1，$\frac{\sqrt{3}}{4}+\frac{3}{2}$]．

Answer 1

分析 建立空间坐标系，利用向量的基本定理，求出M的坐标，利用线性规划的知识进行求解．

解答 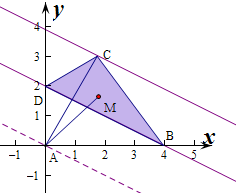解：将四边形ABCD放入坐标系中，
则A（0，0），D（0，2），B（4，0），
∵∠ADC=120°，AD=DC=2，
∴∠DCA=30°，AC=$2\sqrt{3}$，
则C（$\sqrt{3}，3$），
设M（x，y），
∵$\overrightarrow{AM}$=$λ\overrightarrow{AB}$+μ$\overrightarrow{AD}$，
∴（x，y）=λ（4，0）+μ（0，2）=（4λ，2μ），
即x=4λ，y=2μ，
则λ=$\frac{x}{4}$，μ=$\frac{y}{2}$，
则λ+μ=$\frac{x}{4}$+$\frac{y}{2}$，
设z=$\frac{x}{4}$+$\frac{y}{2}$，
则y=$-\frac{x}{2}$+2z，
平移直线y=$-\frac{x}{2}$+2z，
由图象知当直线y=$-\frac{x}{2}$+2z经过点B（4，0）时，截距最小，此时z最小，z=$\frac{4}{4}+0=1$，
当直线y=$-\frac{x}{2}$+2z经过点C（$\sqrt{3}，3$）时，截距最大，此时z最大，
即z=$\frac{\sqrt{3}}{4}+\frac{3}{2}$，
故1≤z≤$\frac{\sqrt{3}}{4}+\frac{3}{2}$，
故λ+μ的取值范围是[1，$\frac{\sqrt{3}}{4}+\frac{3}{2}$]，
故答案为：[1，$\frac{\sqrt{3}}{4}+\frac{3}{2}$]

点评 本题主要考查平面向量基本定理的应用以及线性规划的综合应用，建立坐标系是解决本题的关键．综合性较强，难度较大．