
分析 (Ⅰ)当b=1,写出函数的对称轴,画出函数的图象,从而求出函数的递增区间即可;
(Ⅱ)若函数y=g(x)-$\frac{1}{2}$b在[-2,2]上有三个零点,即函数y=g(x)与y=$\frac{1}{2}$b在[-2,2]上有三个交点,先讨论g(x)=$\left\{\begin{array}{l}{|{x}^{2}-bx-2|,x≥0}\\{{x}^{2}-bx-2,x<0}\end{array}\right.$的图象,对称轴为x=$\frac{1}{2}$b,再结合函数y=g(x)与y=$\frac{1}{2}$b在[-2,2]上有三个交点,即可求实数b的取值范围.
解答 解:(Ⅰ)b=1时:f(x)=x2-x-2=(x-2)(x+1)=$(x-\frac{1}{2})^{2}-\frac{9}{4}$,
画出函数|f(x)|的图象,如图示: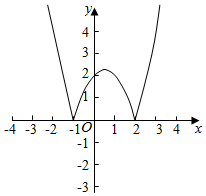
∴f(x)的单调递增区间是(-1,$\frac{1}{2}$),(2,+∞);
(Ⅱ)若函数y=g(x)-$\frac{1}{2}$b在[-2,2]上有三个零点,即函数y=g(x)与y=$\frac{1}{2}$b在[-2,2]上有三个交点,
先讨论g(x)=$\left\{\begin{array}{l}{|{x}^{2}-bx-2|,x≥0}\\{{x}^{2}-bx-2,x<0}\end{array}\right.$的图象,对称轴为x=$\frac{1}{2}$b.
①$\frac{1}{2}$b≤0,即b≤0时,此时,x≥0,f(x)≥0,函数y=g(x)与y=$\frac{1}{2}$b在[-2,2]上最多只有两个交点,不合题意,舍去;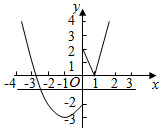
②0<$\frac{1}{2}$b<2,且f(2)=2-2b>0,即0<b<1时,设y=g(x)的图象与x轴的正半轴的交点坐标为(x0,0),而此时函数y=g(x)的图象在[-2.0]上单调递减,在[0,$\frac{1}{2}$b]上单调递增,[$\frac{1}{2}$b,x0]上单调递减,[x0,2]上单调递增,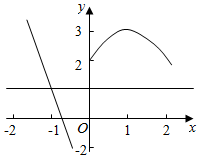
此时f(-2)>|f($\frac{1}{2}$b)|>f(0)>f(2),f(x0)=0,$\frac{1}{2}$b<$\frac{1}{2}$,
∴要使y=g(x)与y=$\frac{1}{2}$b在[-2,2]上有三个交点,则满足:0<$\frac{1}{2}$b≤2-2b,∴0<b≤$\frac{4}{5}$;
③0<$\frac{1}{2}$b<2,且f(2)=2-2b≤0,即1≤b<4时,函数y=g(x)的图象在[-2.0]上单调递减,在[0,$\frac{1}{2}$b]上单调递增,[$\frac{1}{2}$b,2]上单调递减,
此时$\frac{1}{2}$≤$\frac{1}{2}$b<2,∴y=g(x)与y=$\frac{1}{2}$b在[-2,2]上不可能有三个交点;
④$\frac{1}{2}$b≥2,即b≥4时,函数y=f(x)的图象在[-2.0]上单调递减,在[0,2]上单调递增,
∴y=g(x)与y=$\frac{1}{2}$b在[-2,2]上最多只有两个交点,
综上所述,0<b≤$\frac{4}{5}$.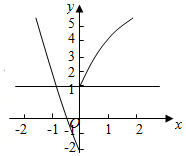
点评 本题考查了二次函数的性质,考查函数的单调性问题,考查图象的交点问题,正确分类讨论是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
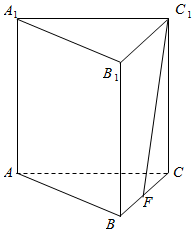 在正三棱柱中,CC1=BC,点F是BC的中点,点 H在线段B1B 上运动.
在正三棱柱中,CC1=BC,点F是BC的中点,点 H在线段B1B 上运动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{125π}{6}$ | B. | $\frac{125π}{24}$ | C. | 25π | D. | $\frac{500π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com