
分析 (1)求导,分类讨论,根据导数与函数单调性的关系,即可求得y=f(x)的单调区间;
(2)由(1)可知,不妨设1<x1<x2,代入ex-ax+a=0,作差,要证x1+x2<2lna,即证${e^{\frac{{{x_1}+{x_2}}}{2}}}<a$,即证$\frac{{{e^{\frac{{{x_2}-{x_1}}}{2}}}-{e^{-\frac{{{x_2}-{x_1}}}{2}}}}}{{{x_2}-{x_1}}}>1$,令$\frac{{{x_2}-{x_1}}}{2}=t>0$,则(*)式化为 et-e-t>2t,构造辅助函数,求导,根据函数的单调性即可求得g(t)>g(0)=0.则x1+x2<2lna.
解答 解:(1)函数f(x)=ex-ax+a,求导,f'(x)=ex-a.
①当a≤0时,f'(x)>0,则函数f(x)为R上的单调递增函数.
②当a>0时,令f'(x)=0,则x=lna.
若x<lna,则f'(x)<0,f(x)在(-∞,lna)上是单调减函数;
若x>lna,则f'(x)>0,f(x)在(lna,+∞)上是单调增函数.
(2)证明:由(Ⅰ)可知,不妨设1<x1<x2,
由$\left\{\begin{array}{l}{e^{x_1}}-a{x_1}+a=0\;\\{e^{x_2}}-a{x_2}+a=0\;\end{array}\right.$两式相减得$a=\frac{{{e^{x_2}}-{e^{x_1}}}}{{{x_2}-{x_1}}}$.
要证x1+x2<2lna,即证${e^{\frac{{{x_1}+{x_2}}}{2}}}<a$,
也就是证${e^{\frac{{{x_1}+{x_2}}}{2}}}<\frac{{{e^{x_2}}-{e^{x_1}}}}{{{x_2}-{x_1}}}$,
即${e^{\frac{{{x_1}+{x_2}}}{2}}}-\frac{{{e^{x_2}}-{e^{x_1}}}}{{{x_2}-{x_1}}}={e^{\frac{{{x_1}+{x_2}}}{2}}}(1-\frac{{{e^{\frac{{{x_2}-{x_1}}}{2}}}-{e^{-\frac{{{x_2}-{x_1}}}{2}}}}}{{{x_2}-{x_1}}})<0$,即证$\frac{{{e^{\frac{{{x_2}-{x_1}}}{2}}}-{e^{-\frac{{{x_2}-{x_1}}}{2}}}}}{{{x_2}-{x_1}}}>1$,
又x2-x1>0,只要证${e^{\frac{{{x_2}-{x_1}}}{2}}}-{e^{-\frac{{{x_2}-{x_1}}}{2}}}>{x_2}-{x_1}$(*).
令$\frac{{{x_2}-{x_1}}}{2}=t>0$,则(*)式化为 et-e-t>2t,
设g(t)=(et-e-t)-2t(t>0)
,g'(t)=(et+e-t)-2>0,所以g(t)在(0,+∞)上单调递增,所以g(t)>g(0)=0.
∴x1+x2<2lna.
点评 本题考查导数的综合应用,考查利用导数求函数的单调性区间及最值,考查转化思想,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{30}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
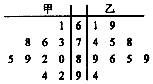 甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如下图所示的茎叶图.规定模拟考试成绩不低于81分为优秀等次.
甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如下图所示的茎叶图.规定模拟考试成绩不低于81分为优秀等次.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
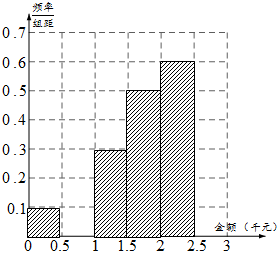 某网络营销部门为了统计某市网友“双11”在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图):
某网络营销部门为了统计某市网友“双11”在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图):| 网购金额 (单位千元) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com