
分析 (I)消参数得到普通方程,将x=ρcosθ,y=ρsinθ代入普通方程得到极坐标方程;
(II)根据导数与切线的关系求出切点P,Q的坐标,得到直线PQ的方程,令m的系数为0得出定点坐标.
解答 解:(I)将x=t代入y=t2+1,得y=x2+1,∴曲线C的普通方程为y=x2+1.
将x=ρcosθ,y=ρsinθ代入y=x2+1得ρsinθ=ρ2cos2θ+1.
∴曲线C的极坐标方程为ρsinθ=ρ2cos2θ+1.
(II)设过A(m,0)的直线y=k(x-m)与曲线y=x2+1相切,切点为(x,y)
则$\left\{\begin{array}{l}{2x=k}\\{y={x}^{2}+1}\\{y=k(x-m)}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=m+\sqrt{{m}^{2}+1}}\\{y=2{m}^{2}+2m\sqrt{{m}^{2}+1}+2}\end{array}\right.$,或$\left\{\begin{array}{l}{x=m-\sqrt{{m}^{2}+1}}\\{y=2{m}^{2}-2m\sqrt{{m}^{2}+1}+2}\end{array}\right.$.
∴直线PQ方程为$\frac{y-(2{m}^{2}-2m\sqrt{{m}^{2}+1}+2)}{4m\sqrt{{m}^{2}+1}}$=$\frac{x-(m-\sqrt{{m}^{2}+1})}{2\sqrt{{m}^{2}+1}}$,即2mx-y+2=0.
显然,当x=0时,y=2.
∴直线PQ过定点(0,2).
点评 本题考查了参数方程,极坐标方程,直角坐标方程的互化,导数与切线的关系,直线方程的应用.


科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | $\frac{1}{8}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (±5,0) | B. | (0,5) | C. | (±$\sqrt{7}$,0) | D. | (0,±$\sqrt{7}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
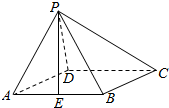 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com