练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知抛物线方程为y2＝4x，直线l的方程为x－y＋5＝0，在抛物线上有一动点P到y轴的距离为d1，到直线l的距离为d2，则d1＋d2的最小值为________．


    3－1


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    求过直线l1：x－2y＋3＝0与直线l2：2x＋3y－8＝0的交点，且到点P(0,4)的距离为2的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设F1，F2分别是椭圆＝1的左、右焦点，点P在椭圆上，若△PF1F2为直角三角形，则△PF1F2的面积等于________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知双曲线的中心在原点，焦点F1，F2在坐标轴上，离心率为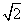，且过点(4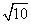，－)．点M(3，m)在双曲线上．

    (1)求双曲线方程；

    (2)求证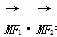：＝0；

    (3)求△F1MF2面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    过点(0,1)作直线，使它与抛物线y2＝4x仅有一个公共点，这样的直线有(　　)

    A．1条                                  B．2条 

    C．3条                                  D．4条

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设动点P在直线x－1＝0上，O为坐标原点，以OP为直角边，点O为直角顶点作等腰直角三角形OPQ，则动点Q的轨迹是(　　)

    A．椭圆                                 B．两条平行直线

    C．抛物线                               D．双曲线

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知真命题：若A为⊙O内一定点，B为⊙O上一动点，线段AB的垂直平分线交直线OB于点P，则点P的轨迹是以O，A为焦点，OB长为长轴长的椭圆．类比此命题，写出另一个真命题：若A为⊙O外一定点，B为⊙O上一动点，线段AB的垂直平分线交直线OB于点P，则点P的轨迹是__________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知平面内一动点P到点F(1,0)的距离与点P到y轴的距离的差等于1.

    (1)求动点P的轨迹C的方程；

    (2)过点F作两条斜率存在且互相垂直的直线l1，l2，设l1与轨迹C相交于点A，B，l2与轨迹C相交于点D，E，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数.他们研究过如图所示的三角形数:

    将三角形数1,3, 6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn},可以推测:

    (1)b2012是数列{an}中的第　　　　项; 

    (2)b2k-1=　　　　.(用k表示) 

    查看答案和解析>>

    同步练习册答案