Question

如图，直三棱柱ABC-A₁B₁C₁中，AC⊥AB，AB=2AA₁，M是AB的中点，△A₁MC₁是等腰三角形，D为CC₁的中点，E为BC上一点．
（1）若DE∥平面A₁MC₁，求

CE

EB

；
（2）平面A₁MC₁将三棱柱ABC-A₁B₁C₁分成两个部分，求较小部分与较大部分的体积之比．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定

专题：综合题,空间位置关系与距离

分析：（1）先证明A₁，M，N，C₁四点共面，利用DE∥平面A₁MC₁，可得DE∥C₁N，利用D为CC₁的中点，即可求

CE

EB

；
（2）将几何体AA₁M-CC₁N补成三棱柱AA₁M-CC₁F，求出几何体AA₁M-CC₁N的体积、直三棱柱ABC-A₁B₁C₁体积，即可求较小部分与较大部分的体积之比．

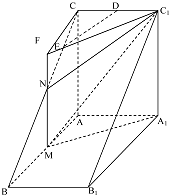
解答： 解：（1）取BC中点为N，连结MN，C₁N，…（1分）
∵M，N分别为AB，CB中点
∴MN∥AC∥A₁C₁，
∴A₁，M，N，C₁四点共面，…（3分）
且平面BCC₁B₁∩平面A₁MNC₁=C₁N
又DE?平面BCC₁B₁，且DE∥平面A₁MC₁
∴DE∥C₁N
∵D为CC₁的中点，
∴E是CN的中点，…（5分）
∴

CE

EB

=

1

3

．                                                 …（6分）
（2）∵三棱柱ABC-A₁B₁C₁为直三棱柱，∴AA₁⊥平面ABC，
又AC⊥AB，则AC⊥平面ABB₁A₁
设AB=2AA₁=2，又三角形A₁MC₁是等腰三角形，所以A1M=A1C1=

2

．
如图，将几何体AA₁M-CC₁N补成三棱柱AA₁M-CC₁F
∴几何体AA₁M-CC₁N的体积为：V1=

1

2

•AM•AA1•AC-

1

3

•

1

2

•CF•CC1•NF=

1

2

×1×1×

2

-

1

3

×

1

2

×1×1×

2

2

=

5 2

12

…（9分）
又直三棱柱ABC-A₁B₁C₁体积为：V=

1

2

×

2

×2×1=

2

…（11分）
故剩余的几何体棱台BMN-B₁A₁C₁的体积为：V2=V-V1=

7 2

12

∴较小部分的体积与较大部分体积之比为：

V1

V2

=

5

7

．                   …（12分）

点评：本题考查直线与平面平行的判定，棱柱、棱锥、棱台的体积，根据题目条件，将问题灵活转化是关键，考查逻辑推理能力与计算能力．