
分析 求出P,Q的坐标,利用$\overrightarrow{QP}$=4$\overrightarrow{P{F}_{1}}$,建立方程向量坐标关系,进行求解即可求出双曲线C的离心率.
解答 解:直线PQ经过B(0,b),F1(-c,0),则kPQ=$\frac{b}{c}$.
∴直线PQ为:y=$\frac{b}{c}$(x+c),与y=$\frac{b}{a}$x.联立得:Q($\frac{ac}{c-a}$,$\frac{bc}{c-a}$);
与y=-$\frac{b}{a}$x.联立得:P(-$\frac{ac}{c+a}$,$\frac{bc}{c+a}$).
∴$\overrightarrow{P{F}_{1}}$=(-c+$\frac{ac}{c+a}$,-$\frac{bc}{a+c}$),$\overrightarrow{QP}$=(-$\frac{ac}{c+a}$-$\frac{ac}{c-a}$,$\frac{bc}{a+c}-\frac{bc}{c-a}$)
∵4$\overrightarrow{P{F}_{1}}$=$\overrightarrow{QP}$,
∴横坐标满足-$\frac{ac}{c+a}$-$\frac{ac}{c-a}$=4(-c+$\frac{ac}{c+a}$),
即$\frac{-2a{c}^{2}}{(c+a)(c-a)}$=$\frac{-4{c}^{2}}{c+a}$,
即$\frac{a}{c-a}$=2,
则a=2c-2a,
则2c=3a,
∴e=$\frac{c}{a}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$
点评 本题主要考查双曲线的离心率的计算,根据条件求出直线方程,联立方程组求出交点坐标,利用向量关系建立a,c的方程是解决本题的关键.考查学生的计算能力.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{9}$=1(x>0) | B. | $\frac{x^2}{16}-\frac{y^2}{9}$=1 | C. | $\frac{x^2}{16}-\frac{y^2}{9}$=1(x<0) | D. | $\frac{x^2}{25}+\frac{y^2}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
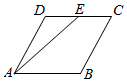
| A. | $\sqrt{7}$ | B. | 5 | C. | $\sqrt{21}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
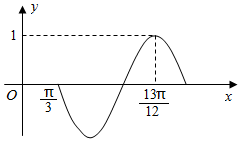 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com