
分析 以D为原点,DA、DC、DD1为x,y,z轴建立空间直角坐标系,
利用坐标表示$|{\overrightarrow{PA}}|=2$,则点P的轨迹是以A为球心,2为半径的球面一部分;
计算$\overrightarrow{P{C}_{1}}$•$\overrightarrow{P{D}_{1}}$=x2+(y-1)2+(z-2)2-1,
它表示点P到点M(0,1,2)的距离的平方再减去1;
由图形知P为AM与所在的球面交点时,$\overrightarrow{P{C_1}}•\overrightarrow{P{D_1}}$的值最小,
求出点P的坐标,利用数量积求出$\overrightarrow{P{C_1}}$与$\overrightarrow{P{D_1}}$的夹角.
解答 解:以D为原点,DA、DC、DD1为x,y,z轴建立空间直角坐标系,
如图所示;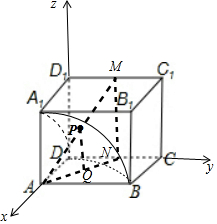
由棱长为2,得A(2,0,0),C1(0,2,2),D1(0,0,2),
设P(x,y,z),
由且$|{\overrightarrow{PA}}|=2$,则(x-2)2+y2+z2=4①,
点P的轨迹表示以A为球心,以2为半径的球面的一部分;
又$\overrightarrow{P{C}_{1}}$=(-x,2-y,2-z),$\overrightarrow{P{D}_{1}}$=(-x,-y,2-z),
∴$\overrightarrow{P{C}_{1}}$•$\overrightarrow{P{D}_{1}}$=x2-2y+y2+(z-2)2
=x2+(y-1)2+(z-2)2-1②,
它表示点P到点M(0,1,2)的距离的平方再减去1;
由图形知,当P为AM与①所在的球面交点时,$\overrightarrow{P{C_1}}•\overrightarrow{P{D_1}}$的值最小,
此时AM=3,AP=2;
∴x=$\frac{2}{3}$,y=$\frac{2}{3}$,z=$\frac{4}{3}$;
∴$\overrightarrow{P{C_1}}•\overrightarrow{P{D_1}}$=${(\frac{2}{3})}^{2}$+${(\frac{2}{3}-1)}^{2}$+${(\frac{4}{3}-1)}^{2}$-1=0,
∴$\overrightarrow{P{C_1}}$与$\overrightarrow{P{D_1}}$夹角为90°.
故答案为:90°.
点评 本题考查了空间直角坐标系与空间向量的应用问题,是较难的题目.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 等于0 | B. | 等于$\frac{π}{6}$ | C. | 等于$\frac{π}{2}$ | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{25}{6}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com