
| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{25}{6}$ | D. | 4 |
分析 作出不等式组对应的平面区域,利用目标函数取得最大值,确定a,b的关系,利用基本不等式求$\frac{1}{a}+\frac{1}{{{b^{\;}}}}$的最小值.
解答 解:作出不等式组对应的平面区域如图:(阴影部分OAC),
由z=ax+by(a>0,b>0),则y=-$\frac{a}{b}$x+$\frac{z}{b}$,
平移直线y=-$\frac{a}{b}$x+$\frac{z}{b}$,由图象可知当直线y=-$\frac{a}{b}$x+$\frac{z}{b}$经过点是,直线的截距最大,此时z最大为2.
由$\left\{\begin{array}{l}{3x-y-2=0}\\{x-y=0}\end{array}\right.$,解得C(1,1),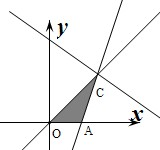
代入目标函数z=ax+by得a+b=2.
∴$\frac{1}{a}+\frac{1}{{{b^{\;}}}}$=$\frac{1}{2}$($\frac{1}{a}+\frac{1}{{{b^{\;}}}}$)(a+b)=$\frac{1}{2}$(1+$\frac{a}{b}$+$\frac{b}{a}$+1)=1+$\frac{1}{2}$($\frac{a}{b}$+$\frac{b}{a}$)≥1+$\sqrt{\frac{a}{b}•\frac{b}{a}}$=2,
当且仅当$\frac{a}{b}$=$\frac{b}{a}$即a=b=1时取等号,
∴$\frac{1}{a}+\frac{1}{{{b^{\;}}}}$的最小值为2.
故选:A.
点评 本题主要考查线性规划的应用,利用数形结合是解决此类问题的基本方法,利用基本不等式的性质可求表达式的最小值.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3x2-2)'=3x | B. | (log2x)'=$\frac{1}{x•ln2}$ | C. | (cosx)'=sinx | D. | ($\frac{1}{lnx}$)'=x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?{x}∈R,\frac{2}{x}+ln{x}<0$ | B. | $?{x}∈R,\frac{2}{x}+ln{x}≤0$ | ||
| C. | $?{x_0}∈R,\frac{2}{x_0}+ln{x_0}<0$ | D. | $?{x_0}∈R,\frac{2}{x_0}+ln{x_0}≤0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com