
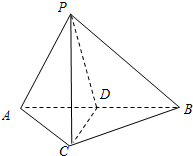
 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.分析 (Ⅰ)根据线面垂直的性质证明PC⊥平面ABC即可证明PC⊥AB;
(Ⅱ)建立空间直角坐标系求出平面的法向量,利用向量法即可求二面角B-AP-C的大小的余弦;
(Ⅲ)利用向量法即可求出点C到平面APB的距离.
解答 证明: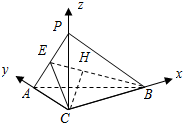 (Ⅰ)∵AC=BC,AP=BP,
(Ⅰ)∵AC=BC,AP=BP,
∴△APC≌△BPC.
又PC⊥AC,∴PC⊥BC.
∵AC∩BC=C,
∴PC⊥平面ABC.
∵AB?平面ABC,
∴PC⊥AB.
(Ⅱ)如图,以C为原点建立空间直角坐标系C-xyz.
则C(0,0,0),A(0,2,0),B(2,0,0).
设P(0,0,t).
∵|PB|=|AB|=2$\sqrt{2}$,
∴t=2,P(0,0,2).
取AP中点E,连结BE,CE.
∵|AC|=|PC|,|AB|=|BP|,
∴CE⊥AP,BE⊥AP.
∴∠BEC是二面角B-AP-C的平面角.
∵E(0,1,1),
∴$\overrightarrow{EC}=(0,-1,-1)$,$\overrightarrow{EB}$=(2,-1,-1),
∴cos$∠BEC=\frac{\overrightarrow{EC}•\overrightarrow{EB}}{|\overrightarrow{EC}||\overrightarrow{EB}|}$=$\frac{2}{\sqrt{2}•\sqrt{6}}=\frac{\sqrt{3}}{3}$.
(Ⅲ)∵AC=BC=PC,
∴C在平面APB内的射影为正△APB的中心H,且CH的长为点C到平面APB的距离.
如(Ⅱ)建立空间直角坐标系C-xyz.
∵BH=2HE,
∴点H的坐标为($\frac{2}{3}$,$\frac{2}{3}$,$\frac{2}{3}$).
∴|$\overrightarrow{CH}$|=$\frac{2\sqrt{3}}{3}$,
∴点C到平APB的距离为$\frac{2\sqrt{3}}{3}$.
点评 本题主要考查空间位置关系的判断,以及利用向量法求二面角的大小以及点到平面的距离,考查学生的推理能力.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | (8,10) | B. | (2$\sqrt{2}$,$\sqrt{10}$) | C. | (2$\sqrt{2}$,10) | D. | ($\sqrt{10}$,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,PA⊥平面ABC,AB⊥BC,AB=PA=2BC=2,M为PB的中点.
如图,PA⊥平面ABC,AB⊥BC,AB=PA=2BC=2,M为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com