
分析 (1)通过函数f(x),得f′(x),然后结合f′(x)与0的关系对a的正负进行讨论即可;
(2)对a的正负进行讨论:当a<0时,f(x)≥b不可能恒成立;当a=0时,此时ab=0; 当a>0时,由题结合(1)得ab≤2a2-a2lna,设g(a)=2a2-a2lna(a>0),问题转化为求g(a)的最大值,利用导函数即可.
解答 解:(1)由函数f(x)=ex-ax+a,可知f′(x)=ex-a,
①当a≤0时,f′(x)>0,函数f(x)在R上单调递增;
②当a>0时,令f′(x)=ex-a=0,得x=lna,
故当x∈(-∞,lna)时,f′(x)<0,此时f(x)单调递减;
当x∈(lna,+∞)时,f′(x)>0,此时f(x)单调递增.
综上所述,当a≤0时,函数f(x)在单调递增区间为(-∞,+∞);
当a>0时,函数f(x)的单调递减区间为(-∞,lna),单调递增区间为(lna,+∞);
(2)由(1)知,当a<0时,函数f(x)在R上单调递增且当x→-∞时,f(x)→-∞,∴f(x)≥b不可能恒成立;
当a=0时,此时ab=0;
当a>0时,由函数f(x)≥b对任意x∈R都成立,可得b≤fmin(x),
∵fmin(x)=2a-alna,∴b≤2a-alna,∴ab≤2a2-a2lna,
设g(a)=2a2-a2lna (a>0),则g′(a)=4a-(2alna+a)=3a-2alna,
由于a>0,令g′(a)=0,得$lna=\frac{3}{2}$,故$a={e}^{\frac{3}{2}}$,
当$a∈(0,{e}^{\frac{3}{2}})$时,g′(a)>0,g(a)单调递增;
当$a∈({e}^{\frac{3}{2}},+∞)$时,g′(a)<0,g(a)单调递减.
所以${g}_{max}(a)=\frac{{e}^{3}}{2}$,即当$a={e}^{\frac{3}{2}}$,$b=\frac{1}{2}{e}^{\frac{3}{2}}$时,ab的最大值为$\frac{{e}^{3}}{2}$.
点评 本题考查函数的单调性及最值,利用导函数来研究函数的单调性是解题的关键,注意解题方法的积累,属于中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:填空题
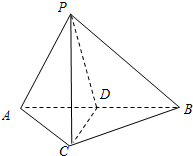 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知点M,N是单位圆的半圆弧$\widehat{AB}$上异于端点的不同的任意两点,且直线MN与x轴相交于点R,若$\overrightarrow{OA}=x\overrightarrow{OM}+y\overrightarrow{ON}$(x,y∈R,O为坐标原点),则实数x+y的取值范围是(-∞,1).
如图,已知点M,N是单位圆的半圆弧$\widehat{AB}$上异于端点的不同的任意两点,且直线MN与x轴相交于点R,若$\overrightarrow{OA}=x\overrightarrow{OM}+y\overrightarrow{ON}$(x,y∈R,O为坐标原点),则实数x+y的取值范围是(-∞,1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 61 | B. | 16 | C. | 81 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com