
分析 (1)由an+1=2an+1,得到an+1+1=2(an+1),分a1=t=-1和a1=t≠-1,说明数列{an+1}是不是等比数列;
(2)①由t=1,得a1+1=2,由等比数列的通项公式求得${a}_{n}={2}^{n}-1$,代入Cn=$\frac{{2}^{n}}{{a}_{n}{a}_{n+1}}$,裂项后可得Cn=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$;
②由Tn=C1+C2+C3+…+Cn,裂项相消求和后得答案.
解答 (1)解:由an+1=2an+1,得an+1+1=2(an+1),
若a1=t=-1,则a1+1=0,数列{an+1}不是等比数列;
若a1=t≠-1,则a1+1≠0,数列{an+1}是首项为t+1,公比为2的等比数列,
(2)证明:①由t=1,则a1+1=2,
∴an+1=2•2n-1=2n,则${a}_{n}={2}^{n}-1$,
∴Cn=$\frac{{2}^{n}}{{a}_{n}{a}_{n+1}}$=$\frac{{2}^{n}}{({2}^{n}-1)({2}^{n+1}-1)}$=$\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n+1}-1}$,即Cn=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$;
②Tn=C1+C2+C3+…+Cn=$(\frac{1}{{a}_{1}}-\frac{1}{{a}_{2}})+(\frac{1}{{a}_{2}}-\frac{1}{{a}_{3}})+…+(\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}})$
=$\frac{1}{{a}_{1}}-\frac{1}{{a}_{n+1}}=1-\frac{1}{{2}^{n+1}-1}<1$.
点评 本题考查了等比关系的确定,考查了裂项相消法求数列的前n项和,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (2)(3) | C. | (3)(4) | D. | (1)(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{1+\sqrt{10}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
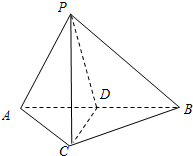 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com