
分析 (Ⅰ)求出直线的斜率,结合直线平行的关系即可,求过点C与直线AB平行的直线方程;
(Ⅱ)根据直线垂直的斜率关系,求出斜率,结合三角形的面积公式进行求解即可.
解答 解:(Ⅰ)∵A(1,4)、B(3,2),
∴直线AB的斜率${k_{AB}}=\frac{4-2}{1-3}=-1$.(2分)
∴过点C与直线AB平行的直线方程为y-1=-(x-1),(4分)
即x+y-2=0. (5分)
(Ⅱ)∵A(1,4)、B(3,2),
∴AB的中点坐标为(2,3).(6分)
又线段AB的垂直平分线的斜率为1,
∴线段AB的垂直平分线的方程为:y-3=1•(x-2)
即x-y+1=0.(8分)
∵M(-1,0),N(1,0),(10分)
∴${S_{△OMN}}=\frac{1}{2}|{OM}|•|{ON}|=\frac{1}{2}$.(12分)
点评 本题主要考查直线斜率公式的求解,以及直线平行和垂直的斜率关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽2m的进出口,如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽2m的进出口,如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
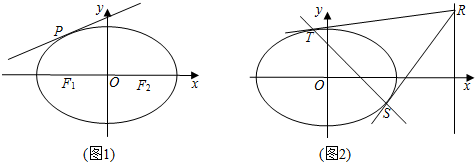
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $\frac{1}{3}$ | C. | 11 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48 | B. | 60 | C. | 72 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com