
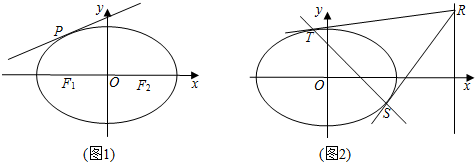
���� ��1������P����Բ�Ķ���˵�λ��ʱ����PF1F2Ϊֱ�������Σ����a��c��ϵʽ���õ������ʣ�
��2����P��x0��y0���Ƴ�$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$���ѣ�x0��y0���������߷��̷��̵�$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$�����з�����$\left\{{\begin{array}{l}{\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}\\{\frac{x_0}{a^2}x+\frac{y_0}{b^2}y=1}\end{array}}\right.$����⼴�ɣ�
��3���������S��x1��y1����T��x2��y2����$R��\frac{a^2}{c}��{y_3}��$���õ�����SR�ķ���Ϊ$\frac{x_1}{a^2}x+\frac{y_1}{b^2}y=1$��
����TR�ķ���Ϊ$\frac{x_2}{a^2}x+\frac{y_2}{b^2}y=1$����$R��\frac{a^2}{c}��{y_3}��$�ֱ�����������̻����Ƴ���S��x1��y1����T��x2��y2����F2��c��0�����㹲�ߣ�Ȼ����ⶨ�����꣮
��� �⣺��$c=\sqrt{{a^2}-{b^2}}$��
��1������P����Բ�Ķ���˵�λ��ʱ����PF1F2Ϊֱ�������Σ�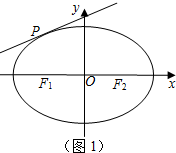
����$a=\sqrt{2}c$����$e=\frac{{\sqrt{2}}}{2}$��
���ԣ���ʱ��Բ��������Ϊ$\frac{{\sqrt{2}}}{2}$��4'
��2����P��x0��y0������Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$�ϣ���$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$��
�ѣ�x0��y0�����뷽��$\frac{x_0}{a^2}x+\frac{y_0}{b^2}y=1$����$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$��
���Ե�P��x0��y0����ֱ��$\frac{x_0}{a^2}x+\frac{y_0}{b^2}y=1$�ϣ���6'
���з�����$\left\{{\begin{array}{l}{\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}\\{\frac{x_0}{a^2}x+\frac{y_0}{b^2}y=1}\end{array}}\right.$����ȥy�ɵ�${a^2}{x^2}-2{a^2}{x_0}x+{a^2}x_0^2=0$��
���x=x0����������ֻ��Ψһ�⣮
���ԣ�ֱ��$\frac{x_0}{a^2}x+\frac{y_0}{b^2}y=1$Ϊ��Բ�ڵ�P�������߷��̡�10'
��3���������S��x1��y1����T��x2��y2����$R��\frac{a^2}{c}��{y_3}��$��
�ɣ�2�����ۿ�֪������SR�ķ���Ϊ$\frac{x_1}{a^2}x+\frac{y_1}{b^2}y=1$��
����TR�ķ���Ϊ$\frac{x_2}{a^2}x+\frac{y_2}{b^2}y=1$�ڡ�12'
��$R��\frac{a^2}{c}��{y_3}��$�ֱ���뷽�̢١��ڣ��ɵ�$\frac{x_1}{c}+\frac{y_1}{b^2}{y_3}=1$��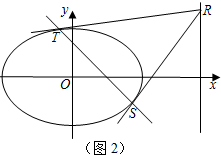
��$\frac{x_2}{c}+\frac{y_2}{b^2}{y_3}=1$��
�ɢۡ�����ʽ����ȥy3���ɵã�x1-c��y2=��x2-c��y1��
����x1-c����y2-0��=��x2-c����y1-0����
���ԣ���S��x1��y1����T��x2��y2����F2��c��0�����㹲�ߣ�
���ԣ�ֱ��ST�������㣬��������Ϊ${F_2}��\sqrt{{a^2}-{b^2}}��0��$��16'
���� ���⿼����Բ�ļ����ʣ���Բ�����߷��̵�Ӧ�ã�ֱ������Բ��λ�ù�ϵ���ۺ�Ӧ�ã�����ת��˼���Լ�����������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����������A-BCD�У�AD��ƽ��BCD��BC��CD��M��AD���е㣬P��BM���е㣬��Q���߶�AC�ϣ���AQ=3QC��
��ͼ����������A-BCD�У�AD��ƽ��BCD��BC��CD��M��AD���е㣬P��BM���е㣬��Q���߶�AC�ϣ���AQ=3QC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1����3�� | B�� | ��1����4�� | C�� | ��2����3�� | D�� | ��2����4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��������C��y2=x��ֱ��l����A��B���㣨����ԭ��O������ABΪֱ����Բǡ�þ���ԭ��O��
��������C��y2=x��ֱ��l����A��B���㣨����ԭ��O������ABΪֱ����Բǡ�þ���ԭ��O���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com