
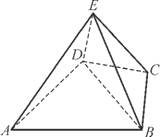
如图,几何体E ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(1) 求证:BE=DE;
(2) 若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
科目:高中数学 来源: 题型:
中心在原点、焦点在x轴上的椭圆C的焦距为2,两准线间的距离为10.设点A(5,0),过点A作直线l交椭圆C于P,Q两点,过点P作x轴的垂线交椭圆C于另一点S.
(1) 求椭圆C的方程;
(2) 求证:直线SQ过x轴上一定点B;
(3) 若过点A作直线与椭圆C只有一个公共点D,求过B,D两点、且以AD为切线的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知一船以15 km/h的速度向东航行,船在A处看到一个灯塔M在北偏东60°方向,行驶4 h后,船到达B处,看到这个灯塔在北偏东15°方向,这时船与灯塔的距离为 km.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列命题:
①若一个平面经过另一个平面的垂线,则这两个平面相互垂直;
②若一个平面内的两条直线与另一个平面都平行,则这两个平面相互平行;
③若两条平行直线中的一条垂直于直线m,则另一条直线也垂直于直线m;
④若两个平面垂直,则一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中真命题为 .(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
现有如下命题:
①过平面外一点有且只有一条直线与该平面垂直;
②过平面外一点有且只有一条直线与该平面平行;
③如果两个平行平面和第三个平面相交, 那么所得的两条交线平行;
④如果两个平面相互垂直, 那么经过第一个平面内一点且垂直于第二个平面的直线必在第一个平面内.则所有真命题的序号是 .(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的前n项和为Sn,且点(n,Sn)在函数y=2x+1-2的图象上.
(1) 求数列{an}的通项公式;
(2) 设数列{bn}满足:b1=0,bn+1+bn=an(n∈N*),求数列{bn}的前n项和公式;
(3) 在第(2)问的条件下,若对于任意的n∈N*,不等式bn<λbn+1恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.
(1) 若m=4,求直线l被圆C所截得弦长的最大值;
(2) 若直线l是圆心C下方的切线,当a在(0,4]上变化时,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com