练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．利用计算机产生0～1之间的均匀随机数x，则事件“3x-2≥0”发生的概率为$\frac{1}{3}$．

    分析 由题意可得概率为线段长度之比，计算可得．

    解答 解：由题意可得总的线段长度为1-0=1，
    在其中满足3x-2≥0即x≥$\frac{2}{3}$的线段长度为1-$\frac{2}{3}$=$\frac{1}{3}$，
    ∴所求概率P=$\frac{1}{3}$，
    故答案为：$\frac{1}{3}$．

    点评 几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．如图，茎叶图记录了某校“春季运动会”甲、乙两名运动员的成绩，他们的平均成绩均为82分，则x+y=（　　）
    A．4B．5C．6D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．PM2.5是指空气中直径小于或等于2.5微米的颗粒物（也称可入肺颗粒物）．为了探究车流量与PM2.5的浓度是否相关，现采集到某城市周一至周五某一时间段车流量与PM2.5得数据如下表：
    时间周一周二周三周四周五
    车流量x（万辆）5051545758
    PM2.5的浓度y（微克/立方米）6970747879
    （Ⅰ）根据上表数据求出y与x的线性回归直线方程$\hat y=\hat bx+\hat a$，
    （Ⅱ）若周六同一时间段车流量是25万辆，试根据（Ⅰ）中求出的线性回归方程预测此时PM2.5的浓度是多少？（保留整数）
    参考公式其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$：方程$\hat y=\hat bx+\hat a$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．若变量x，y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤4}\\{y≥1}\end{array}\right.$，则z=$\frac{1}{2}$x+y的取值范围为[$\frac{3}{2}$，3]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．设z（1+i）=i，则|z|=（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{3}}{2}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．为了解某班学生喜好体育运动是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
    已知喜好体育运动与否，采用分层抽样法抽取容量为10的样本，则抽到喜好体育运动的人数为6．
    （1）请将上面的列联表补充完整；
    （2）能否在犯错误的概率不超过0.005的前提下认为喜好体育运动与性别有关？说明你的理由；
    喜好体育运动不喜好体育运动合计
    男生5
    女生10
    合计50
    下面的临界值表供参考：
    P（k2≥k）0.150.100.050.0250.0100.0050.001
    k2.0722.7063.8415.0246.6357.87910.828
    （参考公式：K2=$\frac{n（ad-bc）^2}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．下列函数中，在区间（0，+∞）上为增函数的是（　　）
    A．y=$\frac{1}{x}$B．y=-x2C．y=（$\frac{1}{2}$）xD．y=log2x

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=sin（ωx+φ），ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$，相邻两对称轴间的距离为π，若将y=f（x）的图象向右平移$\frac{π}{6}$个单位，所得的函数y=g（x）为奇函数．
    （Ⅰ）求函数y=f（x）的解析式；
    （Ⅱ）若关于x的方程2[g（x）]2-m[g（x）]+1=0在区间[0，$\frac{π}{2}$]上有两个不相等的实根，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

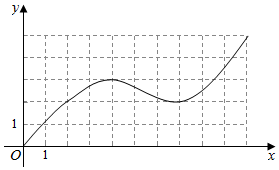    6．已知函数y=f（x）的图形如图所示，给出y=f（x）与x=10和x轴所围成图形的面积估计值；要想得到误差不超过1的面积估计值，可以怎么做？

    查看答案和解析>>

    同步练习册答案