
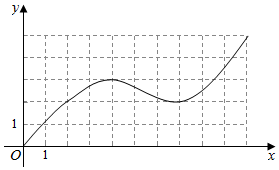
 已知函数y=f(x)的图形如图所示,给出y=f(x)与x=10和x轴所围成图形的面积估计值;要想得到误差不超过1的面积估计值,可以怎么做?
已知函数y=f(x)的图形如图所示,给出y=f(x)与x=10和x轴所围成图形的面积估计值;要想得到误差不超过1的面积估计值,可以怎么做? 分析 设f(x)=ax3+bx2+cx+d,利用待定系数法确定函数关系式,利用定积分求出面积估计值;若要误差小可分段求出f(x)的解析式,然后使用定积分求出面积.
解答 解:设f(x)=ax3+bx2+cx+d,则f′(x)=3ax2+2bx+c,
由图象可知$\left\{\begin{array}{l}{f(0)=0}\\{f(1)=1}\\{f′(4)=0}\\{f′(7)=0}\end{array}\right.$,即$\left\{\begin{array}{l}{d=0}\\{a+b+c=0}\\{\frac{c}{3a}=28}\\{-\frac{2b}{3a}=11}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{2}{137}}\\{b=-\frac{33}{137}}\\{c=\frac{168}{137}}\\{d=0}\end{array}\right.$,
∴f(x)=$\frac{2}{137}$x3-$\frac{33}{137}$x2+$\frac{168}{137}$x.
∴S=${∫}_{0}^{10}$f(x)dx=($\frac{2}{137}×\frac{{x}^{4}}{4}$-$\frac{33}{137}$×$\frac{{x}^{3}}{3}$+$\frac{168}{137}$×$\frac{{x}^{2}}{2}$)|$\left.\begin{array}{l}{10}\\{0}\end{array}\right.$≈17.5.
若要想得到误差不超过1的面积估计值,
可使用分段函数求出f(x)的解析式,然后使用定积分求出面积.
点评 本题考查了定积分在求面积中的应用,求出f(x)的解析式是关键.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1-2\sqrt{6}}{6}$ | B. | -$\frac{1+2\sqrt{6}}{6}$ | C. | $\frac{1+2\sqrt{6}}{6}$ | D. | ±$\frac{1+2\sqrt{6}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
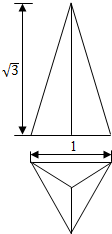
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com