
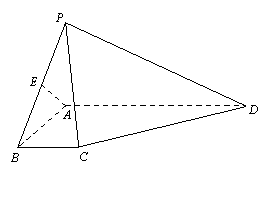
如图,PA⊥平面ABCD,AD//BC,∠ABC=90°,AB=BC=PA=1,AD=3,E是PB的中点.
(1)求证:AE⊥平面PBC;
(2)求二面角B-PC-D的余弦值.
 |
(1)根据题意,建立如图所示的空间直角坐标系,
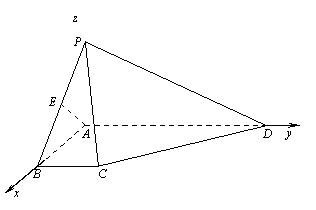 则A(0,0,0),B(1,0,0),C(1,1,0),
则A(0,0,0),B(1,0,0),C(1,1,0),
D(0,3,0),P(0,0,1),E(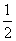 ,0,
,0,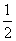 ),
),
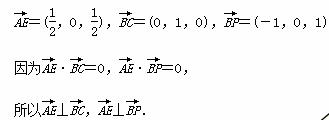 所以AE⊥BC,AE⊥BP.
所以AE⊥BC,AE⊥BP.
因为BC,BP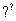 平面PBC,且BC∩BP=B,
平面PBC,且BC∩BP=B,
所以AE⊥平面PBC.
(2)设平面PCD的法向量为n=(x,y,z),则n· =0,n·
=0,n·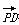 =0.
=0.
因为 =(-1,2,0),
=(-1,2,0),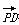 =(0,3,-1),所以-x+2y=0,3y-z=0.
=(0,3,-1),所以-x+2y=0,3y-z=0.
令x=2,则y=1,z=3.
所以n=(2,1,3)是平面PCD的一个法向量.
因为AE⊥平面PBC,所以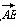 是平面PBC的法向量.
是平面PBC的法向量.
 根据图形可知,二面角B-PC-D的余弦值为-
根据图形可知,二面角B-PC-D的余弦值为-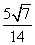 .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
在平面直角坐标系中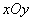 ,已知椭圆
,已知椭圆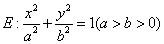 过点
过点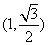 ,且椭圆
,且椭圆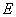 的离心率为
的离心率为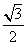 .
.
(1)求椭圆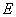 的方程;
的方程;
(2)是否存在以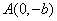 为直角顶点且内接于椭圆
为直角顶点且内接于椭圆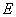 的等腰直角三角形?若存在,求出共有几个;若不存在,请说明理由.
的等腰直角三角形?若存在,求出共有几个;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
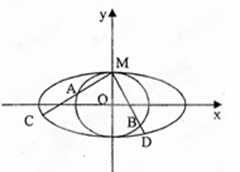
如图,圆O与离心率为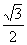 的椭圆T:
的椭圆T: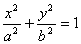 (
(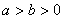 )相切于点M
)相切于点M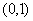 .
.
⑴求椭圆T与圆O的方程;
⑵过点M引两条互相垂直的两直线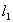 、
、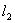 与两曲线分别交于点A、C与点B、D(均不重合).
与两曲线分别交于点A、C与点B、D(均不重合).
①若P为椭圆上任一点,记点P到两直线的距离分别为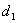 、
、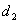 ,求
,求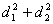 的最大值;
的最大值;
②若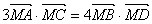 ,求
,求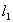 与
与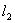 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
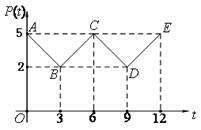
由一个小区历年市场行情调查得知,某一种蔬菜在一年12个月内每月销售量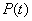 (单位:吨)与上市时间
(单位:吨)与上市时间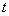 (单位:月)的关系大致如图(1)所示的折线
(单位:月)的关系大致如图(1)所示的折线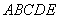 表示,销售价格
表示,销售价格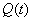 (单位:元/千克)与上市时间
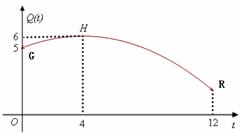
(单位:元/千克)与上市时间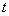 (单位:月)的大致关系如图(2)所示的抛物线段
(单位:月)的大致关系如图(2)所示的抛物线段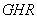 表示(
表示(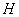 为顶点).
为顶点).
(1)请分别写出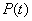 ,
,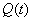 关于
关于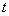 的函数关系式,并求出在这一年内3到6月份的销售额最大的月份?
的函数关系式,并求出在这一年内3到6月份的销售额最大的月份?
(2)图(1)中由四条线段所在直线围成的平面区域为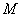 ,动点
,动点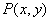 在
在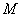 内(包括边界),求
内(包括边界),求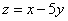 的最大值;
的最大值;
(3) 由(2),将动点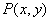 所满足的条件及所求的最大值由加法运算类比到乘法运算(如
所满足的条件及所求的最大值由加法运算类比到乘法运算(如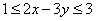 类比为
类比为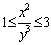 ),试列出
),试列出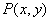 所满足的条件,并求出相应的最大值.
所满足的条件,并求出相应的最大值.
(图1) (图2)
查看答案和解析>>
科目:高中数学 来源: 题型:
《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样的一道题目:把 个面包分给
个面包分给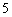 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的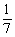 是较小的两份之和,则最小
是较小的两份之和,则最小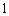 份为( )
份为( )
A.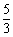 B.
B.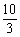 C.
C.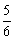 D.
D.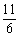
查看答案和解析>>
科目:高中数学 来源: 题型:
已知定义在区间(0,+∞)上的函数f(x)满足f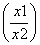 =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1, f(x)在区间上是否存在最小值,若不存在说明理由,若存在求出最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com