
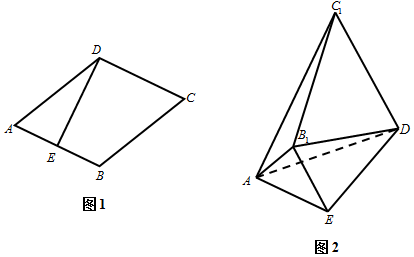
分析 (Ⅰ)由原图形中的DE⊥AB,可得折起后DE⊥AE,DE⊥B1E,再由线面垂直的判定可得DE⊥平面AEB1,进一步得到平面ADE⊥平面AEB1;
(Ⅱ)通过解三角形求出三角形ADB1 的面积,利用等积法求得E到平面ADB1 的距离,再由比例关系求得C1到平面ADB1 的距离,则三棱锥C1-AB1D的体积可求.
解答 证明:(Ⅰ)∵图1,四边形ABCD是菱形,且∠A=60°,E为AB的中点,
∴DE⊥AB,
∵将四边形EBCD沿DE折起至EDC1B1,如图2,
∴DE⊥AE,DE⊥B1E,
又AE∩B1E=E,∴DE⊥平面AEB1,
∵DE?平面ADE,∴平面ADE⊥平面AEB1;
解:(Ⅱ)由(Ⅰ)知,DE⊥AE,DE⊥B1E,∴∠AEB1 为二面角A-DE-C1的平面角为$\frac{π}{3}$,又∵AE=EB1=1,∴△AEB1 为正三角形,则AB1=1.
在RtDEB1 中,由${B}_{1}E=1,DE=\sqrt{3}$,可得B1D=2,
∴△ADB1是等腰三角形,底边AB1 上的高等于$\sqrt{{2}^{2}-(\frac{1}{2})^{2}}=\frac{\sqrt{15}}{2}$.
则${S}_{△AD{B}_{1}}=\frac{1}{2}×1×\frac{\sqrt{15}}{2}=\frac{\sqrt{15}}{4}$.
设E到平面ADB1的距离为h,则由等积法得:$\frac{1}{3}×\frac{\sqrt{15}}{4}h=\frac{1}{3}×\frac{1}{2}×1×\frac{\sqrt{3}}{2}×\sqrt{3}$,
得h=$\frac{\sqrt{15}}{5}$.
∵C1D∥B1E,且C1D=2B1E,
∴C1 到平面ADB1 的距离为$\frac{2\sqrt{15}}{5}$.
则${V}_{{C}_{1}-A{B}_{1}D}=\frac{1}{3}×\frac{\sqrt{15}}{4}×\frac{2\sqrt{15}}{5}=\frac{1}{2}$.
点评 本题考查平面与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | y=g(x)的最小正周期为π | B. | y=g(x)的图象关于直线x=$\frac{π}{6}$对称 | ||
| C. | y=g(x)在[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递增 | D. | y=g(x)的图象关于点($\frac{5π}{12}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
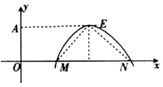 已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,点M的坐标为(1,0)且△MNE为等腰直角三角形,当A取最大值时,f($\frac{1}{3}$)等于( )
已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,点M的坐标为(1,0)且△MNE为等腰直角三角形,当A取最大值时,f($\frac{1}{3}$)等于( )| A. | -$\frac{\sqrt{3}}{4}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
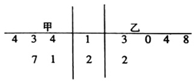 2017年3月2日至16日,全国两会在北京召开,甲、乙两市近5年与会代表名额数统计如图所示,设甲、乙的数据平均数分别为$\overline{{x}_{1}}$,$\overline{{x}_{2}}$,中位数分别为y1,y2,则( )
2017年3月2日至16日,全国两会在北京召开,甲、乙两市近5年与会代表名额数统计如图所示,设甲、乙的数据平均数分别为$\overline{{x}_{1}}$,$\overline{{x}_{2}}$,中位数分别为y1,y2,则( )| A. | $\overline{{x}_{1}}$>$\overline{{x}_{2}}$,y1>y2 | B. | $\overline{{x}_{1}}$>$\overline{{x}_{2}}$,y1=y2 | C. | $\overline{{x}_{1}}$<$\overline{{x}_{2}}$,y1=y2 | D. | $\overline{{x}_{1}}$<$\overline{{x}_{2}}$,y1<y2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com