
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
 =0,椭圆C:
=0,椭圆C: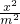 +y2=1,F1、F2分别为椭圆C的左、右焦点.
+y2=1,F1、F2分别为椭圆C的左、右焦点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
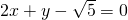 上一点P(x,y)的“折线距离”的最小值是________.
上一点P(x,y)的“折线距离”的最小值是________.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
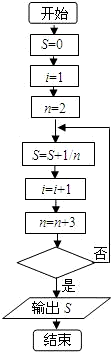 为了计算
为了计算 +
+ +
+ +
+ +…+
+…+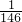 的值,设计了如图所示的程序框图,则下列四个选项中不能做为程序框图中空白判断框内条件的是
的值,设计了如图所示的程序框图,则下列四个选项中不能做为程序框图中空白判断框内条件的是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com