
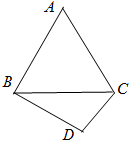
 在△ABC中,角A,B,C的对边分别为a,b,c,满足$\sqrt{3}a=b(sinC+\sqrt{3}cosC)$.
在△ABC中,角A,B,C的对边分别为a,b,c,满足$\sqrt{3}a=b(sinC+\sqrt{3}cosC)$.分析 (1)利用两角和的正弦函数公式及三角形内角和定理化简已知可得tanB=$\sqrt{3}$,由B∈(0,π),即可求得B的值.
(2)由已知利用余弦定理可求BC2=5-4cosD.利用三角形面积公式可求S△ABC=$\frac{5\sqrt{3}}{4}$-$\sqrt{3}$cosD,
S△BDC=sinD,根据三角函数恒等变换的应用可得S四边形ABDC=$\frac{5\sqrt{3}}{4}$+2sin(D-$\frac{π}{3}$),利用正弦函数的图象和性质可求其最大值.
解答 (本题满分为12分)
解:(1)∵$\sqrt{3}a=b(sinC+\sqrt{3}cosC)$.
∴由正弦定理可得:$\sqrt{3}$sinA=sinBsinC+$\sqrt{3}$sinBcosC,…(2分)
∵sinA=sin(B+C)=sinBcosC+sinCcosB,
∴可得:$\sqrt{3}$sinBcosC+$\sqrt{3}$sinCcosB=sinBsinC+$\sqrt{3}$sinBcosC,
可得:$\sqrt{3}$sinCcosB=sinBsinC,
∵sinC≠0,解得sinB=$\sqrt{3}$cosB,即:tanB=$\sqrt{3}$,
∴由B∈(0,π),可得:B=$\frac{π}{3}$. …(6分)
(2)在△BCD中,DB=2,DC=1,
∴BC2=12+22-2×1×2×cosD=5-4cosD. …(7分)
又$∠A=\frac{π}{3}$,由(1)可知△ABC为等边三角形,…(8分)
∴S△ABC=$\frac{\sqrt{3}}{4}$BC2=$\frac{\sqrt{3}}{4}$×(5-4cosD)=$\frac{5\sqrt{3}}{4}$-$\sqrt{3}$cosD,…(9分)
又∵S△BDC=$\frac{1}{2}×BD×CD×sinD$=sinD,…(10分)
∴S四边形ABDC=$\frac{5\sqrt{3}}{4}$-$\sqrt{3}$cosD+sinD=$\frac{5\sqrt{3}}{4}$+2sin(D-$\frac{π}{3}$). …(11分)
∴当D=$\frac{5π}{6}$时,四边形ABDC的面积有最大值,最大值为$\frac{5\sqrt{3}}{4}$+2.…(12分)
点评 本题主要考查了正弦定理、余弦定理、三角形面积公式及三角恒等变换等基础知识的应用,考查了运算求解能力,考查了化归与转化思想,属于中档题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:解答题
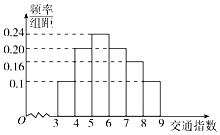 随着社会发展,襄阳市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从襄阳市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:
随着社会发展,襄阳市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从襄阳市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,5] | B. | $[{5,\frac{35}{4}}]$ | C. | $[{0,\frac{35}{4}}]$ | D. | [0,9] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2-i}{10}$ | B. | $\frac{1+i}{10}$ | C. | $\frac{4+7i}{10}$ | D. | $\frac{4-i}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知正三棱柱ABC-A1B1C1所有棱长均为2,D、E分别是BC、BB1中点.
已知正三棱柱ABC-A1B1C1所有棱长均为2,D、E分别是BC、BB1中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com