
 ��֪��R��x0��y0���ڦ���y2=4x�ϣ���RΪ�е�Ħ������ߵ�б��Ϊ$\frac{2}{{y}_{0}}$��������һ��A��-2��-1����������������AB��AC���е�ΪB��C����ƽ����BC�Ħ������ߣ�DΪ�е㣩�ֱ�AB��AC�ڵ�M��N����ͼ����
��֪��R��x0��y0���ڦ���y2=4x�ϣ���RΪ�е�Ħ������ߵ�б��Ϊ$\frac{2}{{y}_{0}}$��������һ��A��-2��-1����������������AB��AC���е�ΪB��C����ƽ����BC�Ħ������ߣ�DΪ�е㣩�ֱ�AB��AC�ڵ�M��N����ͼ�������� ��1����B��$\frac{{{y}_{1}}^{2}}{4}$��y1����C��$\frac{{{y}_{2}}^{2}}{4}$��y2����������ɵ����ߵ�б�ʣ����������б�ʹ�ʽ�����㼴�ɵõ�����B��C�����ꣻ
��2�����BC��б�ʣ���D��$\frac{{m}^{2}}{4}$��m����������ߵ�б�ʣ��ɵ�D�����꣬���ֱ��BC�ķ��̣������е����깫ʽ�ɵ�A����D�ĶԳƵ���ֱ��BC�ϣ����ɵ�֤��
��3��������ɵã�MNΪ������ABC����λ�ߣ���EΪBC���е㣬DΪMN���е㣬���������ABC����������������ε����֮�����Ӧ�ߵıȵĹ�ϵ���ɵ����������������ġ����������Ρ������������$\frac{1}{4}$SΪ���$\frac{1}{4}$Ϊ���ȵĵȱ����У�������������ȱ����е����ʽ���ɵ���������ͣ����ɵõ��������T��
��� �⣺��1����B��$\frac{{{y}_{1}}^{2}}{4}$��y1����C��$\frac{{{y}_{2}}^{2}}{4}$��y2����
������ɵ���BΪ�е�Ħ������ߵ�б��Ϊ$\frac{2}{{y}_{1}}$��
�������б�ʹ�ʽ�ɵ�kAB=$\frac{{y}_{1}+1}{\frac{{{y}_{1}}^{2}}{4}+2}$=$\frac{2}{{y}_{1}}$��
��Ϊy12+2y1-8=0�����y1=2��-4��ȥ����
ͬ���ɵ�y2=-4��
�ɵ�B��1��2����C��4��-4����
��2��֤�����ɣ�1���ɵ�kBC=$\frac{2+4}{1-4}$=-2��
��D��$\frac{{m}^{2}}{4}$��m�����ɵ�$\frac{2}{m}$=-2�����m=-1��
��D��$\frac{1}{4}$��-1����
ֱ��BC�ķ���Ϊy-2=-2��x-1����
�ɵ�2x+y-4=0��
��A��-2��-1������D�ĶԳƵ�Ϊ��$\frac{1}{2}$+2��-2+1������Ϊ��$\frac{5}{2}$��-1����
����ֱ��BC�ķ��̣���D��AE���е㣻
��3��������ɵã�MNΪ������ABC����λ�ߣ���EΪBC���е㣬
DΪMN���е㣬
��|BC|=$\sqrt{��1-4��^{2}+��2+4��^{2}}$=3$\sqrt{5}$��
A��ֱ��BC�ľ���Ϊd=$\frac{|-4-1-4|}{\sqrt{4+1}}$=$\frac{9}{\sqrt{5}}$��
�ɵá�ABC�����ΪS=$\frac{1}{2}$d•|BC|=$\frac{27}{2}$��
��MNΪ��ABC����λ�ߣ��ɵ�S��AMN=$\frac{1}{4}$S��
��M������ΪMB��MD����BDƽ�е�������ΪFG��
�ɵ�S��MFG=$\frac{1}{4}$S��MBD=$\frac{1}{4}$S��MAD=$\frac{1}{8}$S��MAN=$\frac{1}{32}$S��
���N������ΪNC��ND����CDƽ�е�������ΪKL��
ͬ���ɵ�S��NKL=$\frac{1}{32}$S��
�������������������������Ρ��������Ϊ$\frac{1}{16}$S��
ͬ���ɵã���F��G��K��L�������ĸ������������Ρ��������ȣ�
��Ϊ$\frac{1}{256}$S�����Ϊ$\frac{1}{64}$S��
�����С����������Ρ��������Ϊ��$\frac{1}{4}$S+$\frac{1}{16}$S+$\frac{1}{64}$S+��+$\frac{1}{{4}^{n}}$S+��
=$\frac{\frac{1}{4}S}{1-\frac{1}{4}}$=$\frac{1}{3}$S=$\frac{1}{3}$��$\frac{27}{2}$=$\frac{9}{2}$��
��������BC��Χ�ɵ���Ӱ�������ΪS-$\frac{1}{3}$S=$\frac{2}{3}$S=$\frac{2}{3}$��$\frac{27}{2}$=9��
���� ���⿼��ֱ�ߺ������ߵ�λ�ù�ϵ����Ҫ�����е�����������ֱ�ߵ�б�ʺͷ��̵����ã�ͬʱ���������ε��������ע���������������֮�����Ӧ�ߵıȵĹ�ϵ��������������������һ�����Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 8 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $2\sqrt{2}$ | C�� | $3\sqrt{2}$ | D�� | $2+2\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ������ABC-A1BC�ĵ����ABC�У�CA=CB=2����BCA=90�㣬��AA1=4��M��N�ֱ���A1B1��A1A���е㣮
��ͼ����ֱ������ABC-A1BC�ĵ����ABC�У�CA=CB=2����BCA=90�㣬��AA1=4��M��N�ֱ���A1B1��A1A���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
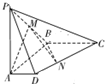 ��ͼ��������P-ABCD�У�����PA�͵���ABCD��AD��BC����ABC=90�㣬PA=AB=BC=2��AD=1��M����PB���е㣮
��ͼ��������P-ABCD�У�����PA�͵���ABCD��AD��BC����ABC=90�㣬PA=AB=BC=2��AD=1��M����PB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 0��l | D�� | 0��-l |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com