
分析 ①将直线方程进行重新整理,利用参数分离法进行求解即可,
②设出M和A点的坐标,由中点坐标公式得到两点坐标的关系,把A的坐标用M的坐标表示,代入圆的方程后整理得答案.
③画出两函数图象,抓住两个关键点,一是直线过点A;一是直线与圆相切,求出相应b的值,即可确定出两集合不为空集时b的范围.
④根据直线与x轴相交,与y轴相离,建立,a,b,c的关系,结合直线的交点坐标进行判断即可.
解答 解:①直线(3+m)x+4y-3+3m=0(m∈R)得m(x+3)+3x+4y-3=0,
由$\left\{\begin{array}{l}{x+3=0}\\{3x+4y-3=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=-3}\\{y=3}\end{array}\right.$,即直线恒过定点(-3,3);故①正确,
②设AB的中点M(x,y),A(x1,y1),
又B(3,4),由中点坐标公式得:$\left\{\begin{array}{l}{\frac{{x}_{1}+3}{2}=x}\\{\frac{{y}_{1}+4}{2}=y}\end{array}\right.$,
即$\left\{\begin{array}{l}{{x}_{1}=2x-3}\\{{y}_{1}=2y-4}\end{array}\right.$.
∵点A在圆x2+y2=4上运动,
∴${{x}_{1}}^{2}+{{y}_{1}}^{2}=4$.
即(2x-3)2+(2y-4)2=4,整理得:${(x-\frac{3}{2})^2}$+(y-2)2=1.
∴线段AB的中点M的轨迹为${(x-\frac{3}{2})^2}$+(y-2)2=1,故②正确,
③集合M表示圆心为原点,半径为1的上半圆,集合N表示直线y=x+b,如图所示,
当直线y=x+b过A点时,把A(1,0)代入得:b=-1;
当直线y=x+b与圆相切,且切点在第二象限时,
圆心到直线的距离d=r,即$\frac{|b|}{\sqrt{2}}$=1,即b=$\sqrt{2}$(负值舍去),
则M∩N≠∅时,实数b的范围是[-1,$\sqrt{2}$].故③错误,
④解:由圆C:(x-b)2+(y-c)2=a2(a>0),得到圆心坐标为(b,c),半径r=a,
∵圆C与x轴相交,与y轴相离,
∴b>a>0,0<c<a,即b-a>0,a-c>0,
联立两直线方程得:$\left\{\begin{array}{l}{ax+by+c=0①}\\{x+y+1=0②}\end{array}\right.$,
由②得:x=-y-1,代入①得:a(-y-1)+by+c=0,
整理得:(b-a)y=a-c,
解得:y=$\frac{a-c}{b-a}$,
∵-a>0,a-c>0,
∴$\frac{a-c}{b-a}$>0,即y>0,
∴x=-y-1<0,
则两直线的交点在第二象限.故④正确,
故答案为:①②④
点评 本题主要考查命题的真假判断,涉及知识点较多,综合性较强,有一定的难度.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
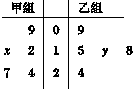 如图茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为5,8.
如图茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为5,8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (-∞,0) | C. | (-1,0] | D. | [-1,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com