
| 2 |
| x2 |
| 4 |
| y2 |
| b2 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 4 |
| y2 |
| b2 |
| x2 |
| 4 |
| y2 |
| b2 |
| 16 |
| b2-4 |
| -16-4b2 |
| b2-4 |
| 2 |
| 16 |
| b2-4 |
| -16-4b2 |
| b2-4 |
| x2 |
| 4 |
| y2 |
| 20 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
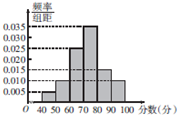 某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为( )
某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为( )| A、120 | B、150 |
| C、180 | D、200 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a+1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OQ |
| PF1 |
| PF2 |
| OT |
| MN |
| OM |
| ON |
| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com