Question

15．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的左，右焦点分别为F₁，F₂，过F₂且倾斜角为45°的直线，双曲线右支交于A，B两点，若△ABF₁为等腰三角形，则该双曲线的离心率为$\frac{\sqrt{14}+\sqrt{2}}{2}$．

Answer 1

分析 由题意不妨设|AF₁|=|AB|，设|AF₂|=m，|BF₂|=n，再由由双曲线的定义可得，|AF₁|=2a+m，|BF₁|=2a+n，在△BF₁F₂中，运用余弦定理，化简整理，结合离心率公式，计算即可得到所求值．

解答 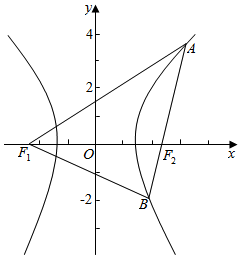解：由题意不妨设|AF₁|=|AB|，
设|AF₂|=m，|BF₂|=n，
由双曲线的定义可得，|AF₁|=2a+m，|BF₁|=2a+n，
即有2a+m=m+n，可得n=2a，
在△BF₁F₂中，由余弦定理可得
（4a）²=（2c）²+（2a）²-2•2c•2a•cos45°，
即为c²-$\sqrt{2}$ac-3a²=0，
由e=$\frac{c}{a}$，可得e²-$\sqrt{2}$e-3=0，
解得e=$\frac{\sqrt{14}+\sqrt{2}}{2}$（$\frac{\sqrt{14}-\sqrt{2}}{2}$舍去）．
故答案为：$\frac{\sqrt{14}+\sqrt{2}}{2}$．

点评 本题考查双曲线的离心率的求法，注意运用双曲线的定义和余弦定理，考查化简整理的运算能力，属于中档题．