
设n∈N*且n≥2,证明:(a1+a2+…+an)2=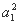 +
+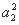 +…+
+…+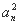 +2[a1(a2+a3+…+an)+a2(a3+a4+…+an)+…+an-1an].
+2[a1(a2+a3+…+an)+a2(a3+a4+…+an)+…+an-1an].
(1) 当n=2时,有(a1+a2)2=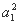 +
+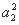 +2a1a2,命题成立.
+2a1a2,命题成立.
(2) 假设当n=k(k≥2)时,命题成立,
即(a1+a2+…+ak)2=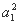 +
+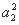 +…+
+…+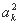 +2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]成立;
+2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]成立;
那么,当n=k+1时,有(a1+a2+…+ak+ak+1)2=(a1+a2+…+ak)2+2(a1+a2+…+ak)ak+1+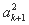 =
=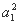 +
+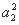 +…+
+…+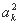 +2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]+2(a1+a2+…+ak)ak+1+
+2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]+2(a1+a2+…+ak)ak+1+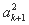 =
=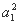 +
+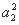 +…+
+…+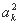 +
+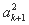 +2[a1(a2+a3+…+ak+ak+1)+a2(a3+a4+…+ak+ak+1)+…+akak+1],
+2[a1(a2+a3+…+ak+ak+1)+a2(a3+a4+…+ak+ak+1)+…+akak+1],
所以当n=k+1时,命题也成立.
根据(1)和(2),可知命题对任意的n∈N*且n≥2都成立.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
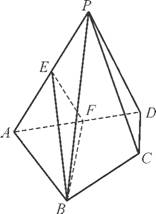
如图,在四棱锥P ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.求证:
ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.求证:
(1) 直线EF∥平面PCD;
(2) 平面BEF⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列四个命题:①{0}是空集;②若a∈N,则-a∉N;③集合{x∈R|x2-2x+1=0}有两个元素;④集合{x∈Q|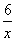 ∈N}是有限集.其中正确命题的个数是( )
∈N}是有限集.其中正确命题的个数是( )
A.1 B.2
C.3 D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com