
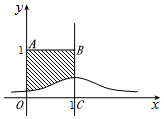
 已知随机变量Z~N(1,1),其正态分布密度曲线如图所示,若向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )
已知随机变量Z~N(1,1),其正态分布密度曲线如图所示,若向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )| A. | 6038 | B. | 6587 | C. | 7028 | D. | 7539 |
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:选择题
| A. | (-3,1] | B. | (1,2) | C. | (-3,0] | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\frac{23}{66}$ | B. | $2\frac{3}{22}$ | C. | $2\frac{61}{66}$ | D. | $1\frac{10}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.
已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,3] | B. | (0,2] | C. | [0,2) | D. | (0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<$\frac{3}{2}$} | B. | {x|x>$\frac{3}{2}$或x<-1} | C. | {x|-$\frac{3}{2}$<x<1} | D. | {x|x>1或x<-$\frac{3}{2}$} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com