
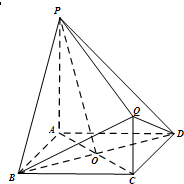
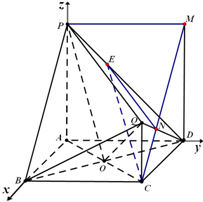
 如图,PA,QC都与正方形ABCD所在平面垂直,AB=PA=2QC=2,AC∩BD=O
如图,PA,QC都与正方形ABCD所在平面垂直,AB=PA=2QC=2,AC∩BD=O| PE |
| ED |
| PE |
| ED |
| CE |
| CE |
 (Ⅰ)证明:连接OQ,由题知PA∥QC,∴P、A、Q、C四点共面,易知BD⊥AC,BD⊥PA,又PA∩AC=A,
(Ⅰ)证明:连接OQ,由题知PA∥QC,∴P、A、Q、C四点共面,易知BD⊥AC,BD⊥PA,又PA∩AC=A,| 2 |
| PA |
| OC |
| AO |
| QC |
| 3 |
| 6 |
| OP |
| BP |
| BQ |
| n |
|
|
| n |
| OP |
| OP |
| n |
| ||||
|
|
| ||
| 6 |
| ||
| 6 |
| PE |
| ED |
| PD |
| PE |
| ED |
| ED |
| ED |
| 1 |
| 1+λ |
| CE |
| CD |
| DE |
| 2 |
| 1+λ |
| 2 |
| 1+λ |
| CE |
| n |
| n |
| CE |
| 2 |
| 1+λ |
| 4 |
| 1+λ |
| 1 |
| 2 |
| PE |
| ED |
| 1 |
| 2 |
| PE |
| ED |
| QN |
| ND |
| QC |
| MD |
| 1 |
| 2 |
| PE |
| ED |
| 1 |
| 2 |


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
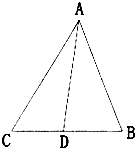 如图,在△ABC中,已知4sin2
如图,在△ABC中,已知4sin2| A-B |
| 2 |
| 1 |
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、已知函数f(x)=
| ||
B、设回归直线方程为
| ||
| C、已知ξ服从正态分布 N(0,σ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.1 | ||
| D、对于命题p:“?x∈R,x2+x+1<0”,则?p:“?x∈R,x2+x+1>0” |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、①简单随机抽样,②系统抽样,③分层抽样 |
| B、①简单随机抽样,②分层抽样,③系统抽样 |
| C、①系统抽样,②简单随机抽样,③分层抽样 |
| D、①分层抽样,②系统抽样,③简单随机抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、cos(A+B)=-cosC | ||||
| B、sin2(A+B)=sin2C | ||||
C、tan
| ||||
D、cos3(A+B)=1-2cos2
|
查看答案和解析>>
科目:高中数学 来源: 题型:
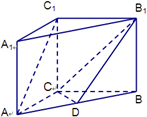 如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com