
���� ��I���������⣬����v��x������ʽΪ�ֶκ�������ʽ���ؼ���������v��x����30��x��180ʱ�ı���ʽ������һ�κ�������ʽ����ʽ���ô���ϵ��������ã�
��II���ɣ���֪����f��x���ı���ʽ���ֶ�����ֵ�����ɵó����ۣ�
��� �⣺����������֪����0��x��30ʱ��v��x��=50��
��30��x��180ʱ����v��x��=ax+b��
����֪�ɵ�$\left\{\begin{array}{l}{180a+b=0}\\{30a+b=50}\end{array}\right.$�����$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=60}\end{array}\right.$��
���Ժ����ԣ�x��=$\left\{\begin{array}{l}{50��}&{0��x��30}\\{-\frac{1}{3}x+60��}&{30��x��180}\end{array}\right.$
�����ɣ���֪f��x��=$\left\{\begin{array}{l}{50x��}&{0��x��30}\\{-\frac{1}{3}{x}^{2}+60x��}&{30��x��180}\end{array}\right.$
��0��x��30ʱ��f��x��=50xΪ��������
�൱x=30ʱ�������ֵΪ1500��
��30��x��180ʱ��f��x��=-$\frac{1}{3}$x2+60x=-$\frac{1}{3}$��x-90��2+2700��
��x=90ʱ�������ֵΪ2700��
���ϣ��������ܶ�Ϊ90��/ǧ��ʱ��������������ֵΪ2700����
���� ������������ܶȵ�ʵ�����⣬�����������ֵ����Ӧ�ij����ܶȣ����ؿ����˺�������ֵ�Ȼ���֪ʶ��ͬʱ����������ѧ֪ʶ���ʵ������������������е��⣮


 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7 | B�� | 8 | C�� | 9 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 6 | C�� | 4 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
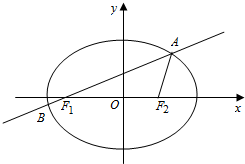 ��ͼ����֪��Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$��������Ϊ$\frac{{\sqrt{2}}}{2}$��F1��F2Ϊ�����ҽ��㣬��F1��ֱ��l����Բ��A��B���㣬��F1AF2���ܳ�Ϊ$2��\sqrt{2}+1��$��
��ͼ����֪��Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$��������Ϊ$\frac{{\sqrt{2}}}{2}$��F1��F2Ϊ�����ҽ��㣬��F1��ֱ��l����Բ��A��B���㣬��F1AF2���ܳ�Ϊ$2��\sqrt{2}+1��$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�DZ߳�Ϊ2���������Σ�AE��ƽ��ABC����AE=1����ƽ��BCD��ƽ��ABC����BD=CD��BD��CD��
��ͼ����ABC�DZ߳�Ϊ2���������Σ�AE��ƽ��ABC����AE=1����ƽ��BCD��ƽ��ABC����BD=CD��BD��CD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ͦ£����ɦ�=m��m��n����n�ͦ���n�ͦ� | |
| B�� | �����Φ£����ɦ�=m���¡ɦ�=n����m��n | |
| C�� | ��m����ֱ�ڦ�����m�����ܴ�ֱ�ڦ��ڵ�������ֱ�� | |
| D�� | �����ɦ�=m��n��m����n�Φ�����n�Φ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com